How to test for difference in means between 5 groups? The variance between the groups are not equal. If they were equal, then I could use ANOVA

Question

There are five groups and I want to test for difference in means between the five groups assuming the variance are not constant between the groups.

Answer 1

One of several possible methods is to use oneway.test in R. Here is an example with three groups, each with ten observations:

x1 = rnorm(10, 100, 10);  x2 = rnorm(10, 95, 15);  x3 = rnorm(10, 90, 5)
x = c(x1, x2, x3); group = rep(1:3, each=10)
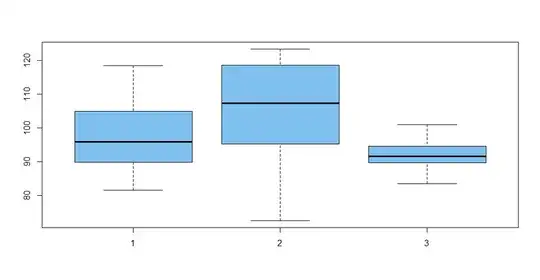
boxplot(x ~ group)

You can see that my fake data were generated with different standard deviations in each of the three groups. The boxplots show this heteroscedasticity. A Bartlett test confirms significance (P-value 0.004).

sd(x1); sd(x2); sd(x3)
[1] 10.88923
[1] 16.35099
[1] 4.656118

bartlett.test(x, group)

        Bartlett test of homogeneity of variances

data:  x and group
Bartlett's K-squared = 11.103, df = 2, p-value = 0.003881

The oneway.test procedure allows for different variances in somewhat the same way as does the Welch 2-sample t test. It indicates that not all group population means are equal (P-value < 5%). Notice that the denominator DF $\approx 15;$ a standard ANOVA assuming equal variances would have denominator DF $= 27.$ [I believe this is the 'Welch ANOVA' suggested by @SalMangiafico.]

mean(x1); mean(x2); mean(x3)
[1] 98.00458
[1] 105.3806
[1] 92.0077

oneway.test(x ~ group)

        One-way analysis of means (not assuming equal variances)

data:  x and group
F = 3.818, num df = 2.000, denom df = 14.536, p-value = 0.04649

You could use Welch 2-sample t tests to explore paired comparisons, perhaps with a Bonferroni family error rate.

Reference: This Q & A mentions a variety of alternative methods.

Answer 2

I would like to recommend generalized least squares as an option. Same way you can create a model for the mean of the data given your predictors, you can also create a model for variance. The gls() function in the nlme package permits us to do this.

I will demo how below:

set.seed(1984)
n <- 25
# Create heteroskedastic data, balanced design
dat <- data.frame(
  y = c(
    rnorm(n, 1, 1), rnorm(n, 0, 1), rnorm(n, .5, 1), 
    rnorm(n, 0, 3), rnorm(n, -.5, 4)),
  groups = sort(rep(LETTERS[1:5], n))
)
boxplot(y ~ groups, dat)

# Assuming all cases have identical variances
summary(aov(y ~ groups, dat))

             Df Sum Sq Mean Sq F value Pr(>F)  
groups        4   69.0  17.255   3.475 0.0101 *
Residuals   120  595.9   4.966                 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# Modeling the error variances
library(nlme)
# This is your standard linear model
coef(summary(fit.gls.baseline <- gls(y ~ groups, dat))))

                 Value Std.Error   t-value      p-value
(Intercept)  1.1784414 0.4457005  2.644021 0.0092875812
groupsB     -0.9748277 0.6303157 -1.546571 0.1246000669
groupsC     -0.8980932 0.6303157 -1.424831 0.1568017302
groupsD     -1.2903790 0.6303157 -2.047195 0.0428223361
groupsE     -2.3076197 0.6303157 -3.661054 0.0003747902

sigma(fit.gls.baseline) # get residual standard deviation
[1] 2.228502

# Next we fit a heteroskedastic model, hidden some output
# varIdent says the variances are identical for cases that have the same value of group
summary(fit.gls <- gls(
  y ~ groups, dat, weights = varIdent(form = ~ 1 | groups)))

Generalized least squares fit by REML
  Model: y ~ groups 
  Data: dat 
       AIC      BIC    logLik
  479.5354 507.4103 -229.7677

Variance function:
 Structure: Different standard deviations per stratum
 Formula: ~1 | groups 
 Parameter estimates:
        A         B         C         D         E 
1.0000000 0.9741804 0.8698579 3.0062743 3.7867899 

Coefficients:
                 Value Std.Error   t-value p-value
(Intercept)  1.1784414 0.1951410  6.038923  0.0000
groupsB     -0.9748277 0.2724316 -3.578248  0.0005
groupsC     -0.8980932 0.2586375 -3.472401  0.0007
groupsD     -1.2903790 0.6182517 -2.087142  0.0390
groupsE     -2.3076197 0.7642898 -3.019299  0.0031

Residual standard error: 0.975705 

A few notes about this model. You will find the residual standard deviation (error) is much less for the heteroskedastic model when compared to the same estimate for the earlier model. Now take a look at the Variance function section, and you will see group A had a standard deviation of 1. These values are relative standard deviations. So the $.976$ reported for the model is the residual SD of group A. $.974 \times .976$ is the value for group B. Groups D $(3 \times .976)$ and E $(3.79 \times .976)$ have much larger residual standard deviations.

Also, let's obtain the heteroskedastic version of the F-test:

# marginal for type III sum of squares, only makes a difference for the
# test of the grouping variable if we have more than one grouping variable
anova(fit.gls, type = "marginal")
Denom. DF: 120 
            numDF  F-value p-value
(Intercept)     1 36.46859  <.0001
groups          4  5.51477   4e-04

Sufficient evidence to suggest that not all groups share the same mean, $F(4, 120)=5.51, p < .001$.

Now to compare the heteroskedastic model to the standard model, note that the coefficients are about the same, however, the standard errors are much smaller for the heteroskedastic model, except for groups D and E. So our p-values are also smaller. A global approach to model comparison would be:

anova(fit.gls, fit.gls.baseline) # Model fit improved
                 Model df      AIC      BIC    logLik   Test  L.Ratio p-value
fit.gls              1 10 479.5354 507.4103 -229.7677                        
fit.gls.baseline     2  6 560.9588 577.6837 -274.4794 1 vs 2 89.42343  <.0001

These results suggest the heteroskedastic model was better, lower AIC, BIC and statistically significant likelihood ratio test.

Now, we do not have access to the data generation process in reality, but we can always plot the boxplt above. Assuming we want to opt for a simpler model, we can assume groups A, B and C have the same variances and groups D and E are different. We can then try:

# Create a variable that classifies the groups according to variance
dat$var.groups <- (dat$groups %in% c("D", "E")) + 0
# then run:
summary(fit.gls.parsim <- gls(
  y ~ groups, dat, weights = varIdent(form = ~ 1 | var.groups)))

Generalized least squares fit by REML
  Model: y ~ groups 
  Data: dat 
       AIC      BIC    logLik
  475.3162 494.8287 -230.6581

Variance function:
 Structure: Different standard deviations per stratum
 Formula: ~1 | var.groups 
 Parameter estimates:
       0        1 
1.000000 3.600023 

Coefficients:
                 Value Std.Error   t-value p-value
(Intercept)  1.1784414 0.1853218  6.358893  0.0000
groupsB     -0.9748277 0.2620846 -3.719516  0.0003
groupsC     -0.8980932 0.2620846 -3.426730  0.0008
groupsD     -1.2903790 0.6924235 -1.863569  0.0648
groupsE     -2.3076197 0.6924235 -3.332671  0.0011

# A model comparison between our previous best and this new model
anova(fit.gls, fit.gls.parsim)
               Model df      AIC      BIC    logLik   Test  L.Ratio p-value
fit.gls            1 10 479.5354 507.4103 -229.7677                        
fit.gls.parsim     2  7 475.3162 494.8287 -230.6581 1 vs 2 1.780859  0.6191

The likelihood ratio test cannot distinguish between this simpler model that has three fewer parameters and our earlier heteroskedastic model. Also AIC and BIC lean towards this model. So we may opt for this model going forward since we do not know the truth. Theory may also suggest certain things about the differences in group variances. One can see how the particular issue of heteroskedasticity can be of substantive interest in itself.

F-test again would be:

anova(fit.gls.parsim, type = "marginal")
Denom. DF: 120 
            numDF  F-value p-value
(Intercept)     1 40.43552  <.0001
groups          4  6.04201   2e-04

Now, the next thing may be contrasts. I do not care much for this in my work, so I do the simplest things here. There are probably better ways to deal with contrasts, see the emmeans package documentation for more options. I just use defaults.

library(emmeans)
pairs(emmeans(fit.gls.parsim, "groups"))
 contrast   estimate        SE  df t.ratio p.value
 A - B     0.9748277 0.2620846 120   3.720  0.0028
 A - C     0.8980932 0.2620846 120   3.427  0.0073
 A - D     1.2903790 0.6924235 120   1.864  0.3427
 A - E     2.3076197 0.6924235 120   3.333  0.0099
 B - C    -0.0767345 0.2620846 120  -0.293  0.9984
 B - D     0.3155513 0.6924235 120   0.456  0.9910
 B - E     1.3327920 0.6924235 120   1.925  0.3099
 C - D     0.3922858 0.6924235 120   0.567  0.9796
 C - E     1.4095265 0.6924235 120   2.036  0.2555
 D - E     1.0172407 0.9435106 120   1.078  0.8174

P value adjustment: tukey method for comparing a family of 5 estimates 

These contrasts use information from the heteroskedastic model as the results would be different if you used the fit.gls.baseline model.

I hope the demonstration above shows how you can account for heteroskedasticity using generalized least squares when performing analysis of variance. Compared to many other approaches, this approach does not simply treat heteroskedasticity as a nuisance. One can also include control variables as in ANCOVA.

---

As an aside, if one also suspects that there is also heteroskedasticity by the control variables in ANCOVA, then the glmmTMB() function in the glmmTMB package can handle this situation. You simply specify a regression equation for the variance using the dispformula = argument.