I understand that using cross validation we can validate our model, but it is also possible that maybe our model is underfitting; hence, providing wrong results. One possibility that I can think of is that if even after making our model less complex results are not right then our model might be underfitting, it is just a guess!
Please write if anything I am missing or any other way to decide whether our model is overfitting or underfitting?
- 43,080
- 1
- 72
- 161
- 81
- 1
- 1
- 2
1 Answers
You can determine the difference between an underfitting and overfitting experimentally by comparing fitted models to training-data and test-data.
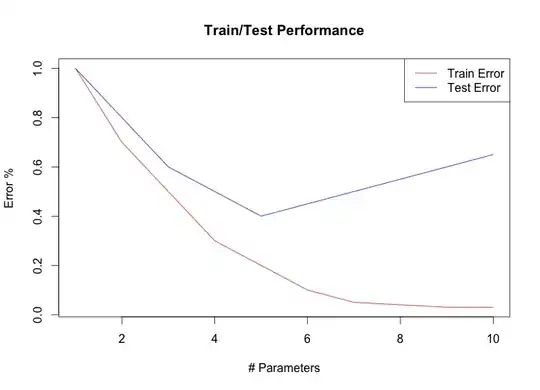
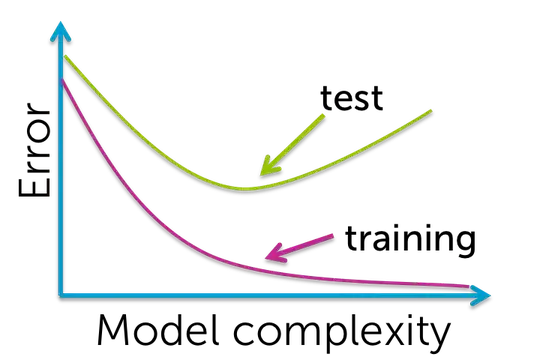
Typical graphs:
These plots will show you the accuracy of the model, as function of some parameter (e.g. 'complexity'), for both the
- training-data (the data use for fitting)
- and test data (data kept separate from the training phase)
One normally chooses the model that does the best on the test-data. If you deviate then for...
For underfitting models, you do worse because they do not capture the true trend sufficiently.
If you get more underfitting then you get both worse fits for training and testing data.
for overfitting models, you do worse because they respond too much to the noise, rather than the true trend.
If you get more overfitting then you get better fits for training data (capturing the noise, but it is useless or even detrimental), but still worse for testing data.
After performing these steps, you should remain in sight that, while you may have selected the least underfitting/overfitting model out of your options, this does not mean that there would not be some other better model.
In particular: the true model, might be an overfitting model in circumstances of high noise-signal ratios (see https://stats.stackexchange.com/a/299523/164061 )
- 43,080
- 1
- 72
- 161
-
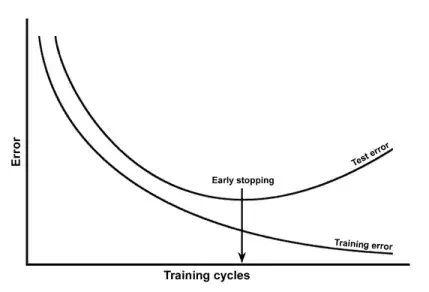
The first plot seems to show error over training time. – Tim Jul 12 '18 at 12:16
-
@Tim Training time makes a model (e.g. an artificial neural network) better in fitting the training data (increases complexity) but not necessarily the testing data. Thus it is related to overfitting vs. underfitting. – Sextus Empiricus Jul 12 '18 at 12:25
-
More direct approach: use a proper accuracy scoring rule (log-likelihood, etc.) to compare the simple model with a model that generalizes the simple model. This assesses adequacy of the simple model. If it's not adequate, it's underfit. – Frank Harrell Jul 12 '18 at 12:46
-
@FrankHarrell log-likelihood may not always be straightforward to express. For GLM and such things with clearly expressible error distributions it is, but beyond that? – Sextus Empiricus Jul 12 '18 at 12:54
-
Log-likelihood and Bayesian counterparts are available in any fully-specified statistical model. This is related to efficient pseudo R^2 measures and AIC. – Frank Harrell Jul 12 '18 at 18:14