4

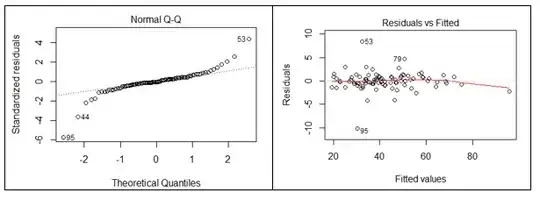
I have a multivariate linear model (y=x1+x2) which gives me the following results when using R's plot() function: enter image description here

I can clearly see that the Normality and Linearity assumptions are not the best. Thus, I decided to add a 2nd degree polynomial variable to the model using poly() (which should give me a model such as y=x1^2+x1+x2) and got the following results: enter image description here

I clearly see an improvement in both assumptions, however, that made me think: can I even do these two tests after I included the polynomial variable? Is the model still considered linear?

Community
  • 1
Riddle-Master
  • 433
  • 3
  • 14
  • 1
    I am not well versed in R's specifics w.r.t. `poly()`, but assuming it adds a term that is polynomial in the _data_, you should be fine. A linear model is linear in the _parameters_, not necessarily in the _data_. – Niels Wouda Jun 20 '18 at 08:51
  • 1
    poly() is used on the model itself, e.i: y~poly(x1,2)+x2. The data stays untouched. – Riddle-Master Jun 20 '18 at 09:29
  • So does it mean that I can't use the plots? – Riddle-Master Jun 20 '18 at 10:28
  • 3
    Yes, the model is still linear (in its parameters and that's what is important here). Yes, you can use these plots. – Roland Jun 20 '18 at 10:57
  • Cool! Can you please explain when it won't longer be considered linear then? Because right now I am confused. – Riddle-Master Jun 20 '18 at 12:00
  • 1
    The term "linear" here has two meanings. One is that the model is a straight line. The other is that linear algebra can directly be used to solve for the coefficients in a technique named "linear regression". One is the name of a mathematical model, one is the name of a mathematical technique. – James Phillips Jun 20 '18 at 13:09
  • 2
    A linear regression model is defined as $\mathbf{y} = X\boldsymbol\beta + \boldsymbol\varepsilon$ where $X$ is the design matrix (all your x-variables) and $\boldsymbol\beta$ is the parameter vector. In the design matrix, a column can be squared values of another column, it won't change this basic, linear model. (Note that `poly` by default creates orthogonal polynomials.) – Roland Jun 20 '18 at 13:22

1 Answers1

2

Is the model still considered linear

To answer your question, recall the definition of a linear model.

Given a dataset composed of a vector $\mathbf{x} = \{ x_1, x_2,...,x_n\}$ of $n$ explanatory variables and one dependent variable $y$ we assume in this model that the relationship between $\mathbf{x}$ and $y$ is linear

$$ y = \beta_0 1 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n + \epsilon$$

Where $\beta_0$ is an intercept term and $\epsilon$ is the error variable, an unobserved random variable that adds "noise" to the linear relationship.

As @Roland points out, the linear relationship must hold in the parameters, not necessarily in the data. So nothing stops you from taking functions of the explanatory variables, and then performing the linear regression again. For example in your case, you could let:

$$ z_1 = x_1, \ z_2 = x_2, \ z_3 = x_1^2, \ z_4 = x_2^2$$

And then perform linear regression on $z$ as:

$$ y = \beta_0 1 + \beta_1 z_1 + \beta_2 z_2 + \beta_3 z_3 + \beta_4 z_4 + \epsilon $$ which is equivalent to

$$ y = \beta_0 1 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1^2 + \beta_4 x_2^2 + \epsilon$$

I clearly see an improvement in both assumptions

If your data shows signs of an underlying polynomial relationship between the explanatory variables, then fitting a linear regression model on polynomial variables will improve your model. As always, this comes with many advantages and disadvantages, some discussed in the posts linked below.

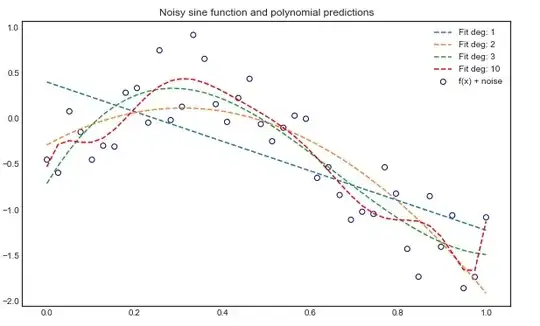
An example

Here is a toy example of trying to fit a linear regression model on a noisy sine curve. As you may know, the sine curve can be approximated by a sum of polynomials, so intuitively we would expect a polynomial linear regression model to do well under certain conditions:

enter image description here

More details

See these excellent posts for more details and explanations

Xavier Bourret Sicotte
  • 7,986
  • 3
  • 40
  • 72