Diagnostic plots for GLMs are very similar to those for LMs, on the grounds that the residuals of GLMs should be homoscedastic, independent of the mean, and asymptotically approach normality, i.e. in the case of large numbers of counts for a Poisson or binomial (this means that such plots are much less useful for Bernoulli (aka binary or binomial with $N=1$; aka standard logistic regression) responses; see e.g. this CV answer.
It's not entirely clear to me why there are separate boot::glm.diag.plots() and underlying boot::glm.diag() functions that overlap a great deal with the built-in stats::plot.lm() (which also handles glm models); my guess is that either the author of the package (A. Canty) had slightly different preferences from the author of stats::plot.lm(), or more likely that the boot package was developed in 1997, when the R project had just begun, and so these functions were written in parallel.
Here are some similarities and differences between plot.lm() and glm.diag.plots():
- Linear predictor (aka "fitted") vs residuals: same as first plot (or
which=1) in plot.lm(), except that glm.diag.plots() uses jackknife deviance residuals, which I can't find defined anywhere (it may be in the Davison and Snell chapter given as a reference in ?glm.diag), but which are computed as sign(dev) * sqrt(dev^2 + h * rp^2) where dev is the deviance residual; h is the hat value; and rp is the standardized Pearson residual (Pearson residual divided by the scale parameter, if there is one, and divided by sqrt(1-h)).
- ordered deviance residuals vs. quantiles of standard normal: "Q-Q plot", same as the third plot (
which=3) in plot.lm(); both use standardized deviance residuals $r_i/(h_i(1-h_i))$, although you have to look in the code to find out.
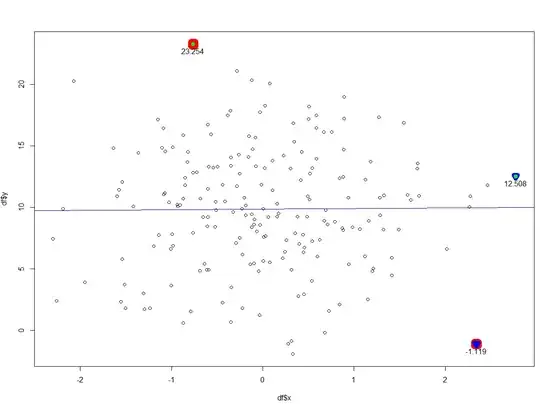
- $h/(1-h)$ vs. Cook statistic: use
which=6 to get this from plot.lm() ($h/(1-h)$ is "leverage"). glm.diag.plots() uses a more conservative rule of thumb to decide which points might be "influential".
- case vs Cook statistic: the same as
which=4 in plot.lm().
plot.lm() seems to have a few advantages, in that it (1) deals more robustly with zero-weight and infinite cases, (2) adds some smoothing lines and contours to the figures to help with interpretation. The car package has some extended functions (e.g. qqPlot), and the DHARMa package uses simulated residuals to get much more interpretable residual plots for logistic regression and other GLMs. mgcv::qq.gam also produces improved Q-Q plots by simulation of residuals.
Your first case looks OK: no obvious pattern, linear Q-Q plot, a couple of "influential" points. I would definitely double-check the two points that have high Cook's distance and linear predictor value of >15 ... I can't really tell from the plot, but it looks like you may have many repeated values in your data?
Second case: same as the first, except that you have a lot more points (so that e.g. the clustering pattern in plot 1 is much stronger). The Q-Q plot looks wonky, but I'm not sure how much I would worry about that. Try with simulated residuals (DHARMa package) ...