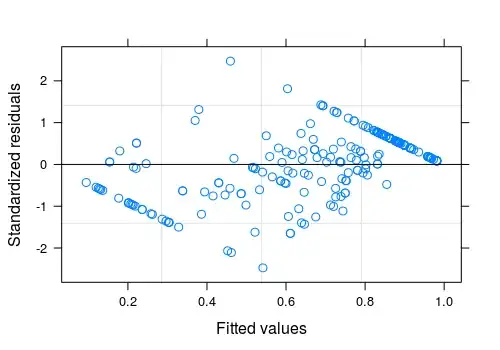
In my particular situation, our outcome variable is recall (bounded between 0 and 1 inclusive), and we are building a linear mixed effects model in R. We end up with a qq plot like the one below:
Is there anything to do to deal with the bounded outcome variable? Any transformations I make will also be bounded, so I don't see how to get around this. Or is the general idea to just do any transformation I can to get the residuals as close to constant variance as possible, and the shape caused by the bounds isn't a big deal?
Some similar questions: