There's a way to do survival analysis of two (or more I suppose) mutually exclusive competing risks as a mixture of two different survival curves. Something like what you see in A.C. Ghani et al. Methods for Estimating the Case Fatality Ratio for a Novel, Emerging Infectious Disease. American Journal of Epidemiology (2005) Vol. 162, No. 5
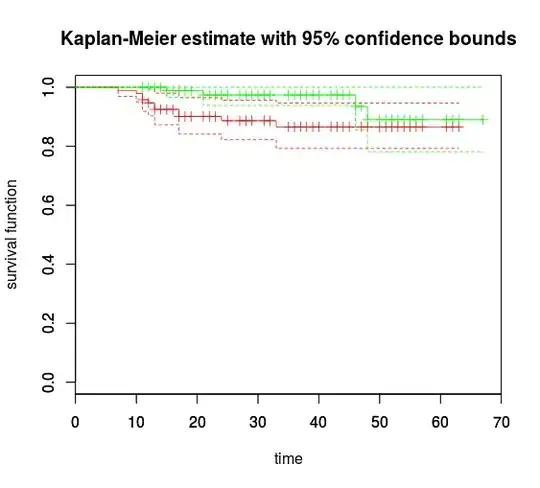
What I'm looking for is a package that would help produce something like this figure:
Where the survival curve of one outcome, and 1-the survival curve of the other outcome will eventually meet at a particular point that is the mixture of the two outcomes.