1

I computed an algorithm to find out the best ARMA (p,q) model via minimisation of the AIC. It turned out ARMA(5,5) is the best one with AIC=-2693.12.

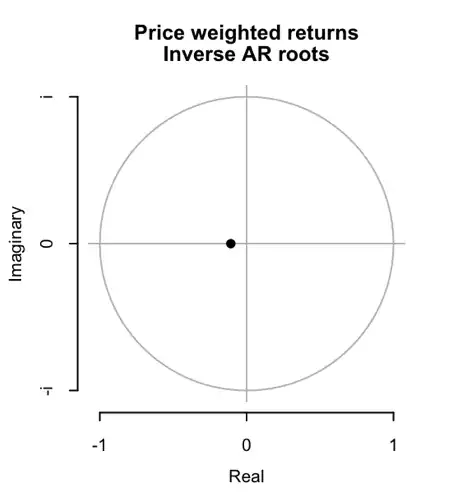
However, the inverse roots of the AR and MA characteristic polynomial are the following:

Inverse AR rootsInverse MA roots

Many of them looks very close to the unitary circle. That makes me feel like I'm in presence of a near non-stationarity & invertibility series (isn't it?). However ACF and PACF show the model as great for capturing autocorrelation in the residuals.

If I use auto.arima() in $R$ to find the best p,q instead, it turns out the best model is a simple AR(1). The AIC worst off to -2687.08.

enter image description here

By looking on internet I figured out that auto.arima() looks yes at AIC (if you specify so) but also at "numerical stability" in returning the "optimal" orders p,q.

What fools me is:

  • What does it mean? What are the implication for a statistical analysis?

,and consequently:

  • Which order should I use? Should I trade some AIC "points" in exchange of much numerical stability proposed by auto.arima()?
  • Would the previous answer change in case the scope of my ARMA model is forecasting or testing?

Here the dput() of my dataset for replicability.

toyo10
  • 71
  • 1
  • 10
  • The models you are suggesting are preposterous to someone who has been bulding minimally sufficient arima models for 50+ years. Please review https://stats.stackexchange.com/questions/319732/i-have-correlogram-acf-and-pacf-below-for-a-temperature-time-series-can-i-say-i/319745#319745 for an extended discussion of the faults of auto.arima primarily due the lack of treatment of deterministic structure – IrishStat May 07 '18 at 13:37
  • Analysis of data can efficiently suggest a possible hybrid model. If you wish to post your data , i will try and elaborate. – IrishStat May 07 '18 at 14:33
  • @ IrishStat thank your for your comment! Cannot copy the `dput()` directly on the post as my post would exceed the character limits. However, you can access it at the end of the (now edited) post. – toyo10 May 07 '18 at 15:15
  • how many observations are there . What is the frequency of measurement ? scale your data way down and post a 1 column csv – IrishStat May 07 '18 at 15:26
  • @IrishStat 1488 daily observations. – toyo10 May 07 '18 at 15:51

1 Answers1

1

I took your 1488 daily values from this economic time series and found an adequate/sufficient model. There are a number of outliers ( only a few shown here ) and the best forecast is a simple constant.enter image description here . The Actual/Fit and Forecast are here enter image description here . The residual ACF suggesting sufficiency is here enter image description here .

Very far from correct but directionally ok is https://people.duke.edu/~rnau/arimrule.htm detailing the way an ARIMA model is formed (IF and only if there are no deterministic structure ( such as pulses) in the data. The acf of the original series is here enter image description here . Your "problem" is that you think auto.arima is a model identification tool ... not so much ! .. It can be under very rare circumstances such as if the following 6 characteristics are true for your data .1 ) no pulses in the the data 2) no step/level shifts in the data .... 3) no seasonal pulses in the data .... 4) no deterministic time trends in the data ... 5) parameters are constant over time .....6 )error variance is constant over time . Unfortunately your data doesn't match the required profile .

IrishStat
  • 27,906
  • 5
  • 29
  • 55