However, these examples feel unnatural because the X′s are typically
covariates and Y is typically a response (at least with the naive
Bayes classifier) (...) it's not clear to me which data generating processes it is best-suited to.
This is not necessarily true. It's easier to think of the Naive Bayes set up as a model where the $X$'s are caused by $Y$. As a canonical example, imagine $Y$ is a disease and $X$ are the symptoms. Your task is to predict the disease (cause) from the symptoms (effects). Then the Naive Bayes model would look like:
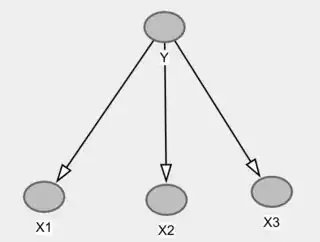
And in this case the $X$'s would be independent conditional on $Y$. Note however, that even in this case the Naive Bayes model is still very simplified, and it suffers from what is usually called the "single-fault" assumption.
I'm interested only in cases where Y is defined as a function of the
covariates.
It's easy to see graphically that this will be very hard to do. If you draw a DAG where the $X$'s are the parents of $Y$, this is what you have now.
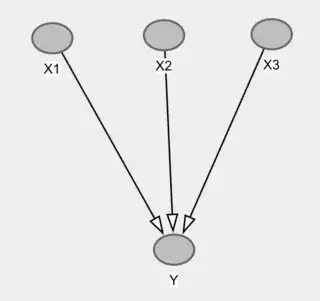
You can see that if you condition on $Y$ we would expect to make all $X$'s dependent, not the opposite. Thus, to create independence this way, you would need to fine-tune the parameters in order to make the $X$ independent conditional on $Y$, despite this structure. That is, you will have to generate a distribution that is unfaithful to the graph.
Thus, if you are trying to predict a consequence from its causes using Naive Bayes, this is a set-up where it's almost guaranteed by construction that the conditional independence of the $X$'s given $Y$ will not hold.
As requested, for an example where conditioning on $Y$ might turn $X_1$ and $X_2$ independent, consider a multivariate normal model, where all variables have unit variance. Let $R_{x_1x_2.y}$ denote the regression coefficient of $X_1$ on $X_2$ controlling for $Y$. We want this coefficient to be zero, and it suffices to make $\sigma_{x_1x_2} = \sigma_{yx_1}\sigma_{yx_2}$. For a numerical example, consider the model $X_1 = U_{X_1}$, $X_2 = 0.25 X_1 + U_{X_2}$ and $Y = 0.4X_1 + 0.4X_2 + U_Y$ where the variances of the disturbances $U$ are adjusted to make the variables have unit variance. This will lead to $\sigma_{x_1x_2} = 0.25$ and $\sigma_{yx_1} = \sigma_{yx_2} = 0.5$, thus $\sigma_{x_1x_2} = \sigma_{yx_1}\sigma_{yx_2} \implies R_{x_1x_2.y} = 0$.

