TL;DR: The warning is not occurring because of complete separation.
library("tidyverse")
library("broom")
# semicolon delimited but period for decimal
ratios <- read_delim("data/W0krtTYM.txt", delim=";")
# filter out the ones with missing values to make it easier to see what's going on
ratios.complete <- filter(ratios, !is.na(ROS), !is.na(ROI), !is.na(debt_ratio))
glm0<-glm(Default~ROS+ROI+debt_ratio,data=ratios.complete,family=binomial)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(glm0)
#>
#> Call:
#> glm(formula = Default ~ ROS + ROI + debt_ratio, family = binomial,
#> data = ratios.complete)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -2.8773 -0.3133 -0.2868 -0.2355 3.6160
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -3.759154 0.306226 -12.276 < 2e-16 ***
#> ROS -0.919294 0.245712 -3.741 0.000183 ***
#> ROI -0.044447 0.008981 -4.949 7.45e-07 ***
#> debt_ratio 0.868707 0.291368 2.981 0.002869 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 604.89 on 998 degrees of freedom
#> Residual deviance: 372.43 on 995 degrees of freedom
#> AIC: 380.43
#>
#> Number of Fisher Scoring iterations: 8
When does that warning occur? Looking at the source code for glm.fit() we find
eps <- 10 * .Machine$double.eps
if (family$family == "binomial") {
if (any(mu > 1 - eps) || any(mu < eps))
warning("glm.fit: fitted probabilities numerically 0 or 1 occurred",
call. = FALSE)
}
The warning will arise whenever a predicted probability is effectively indistinguishable from 1.
The problem is on the top end:
glm0.resids <- augment(glm0) %>%
mutate(p = 1 / (1 + exp(-.fitted)),
warning = p > 1-eps)
arrange(glm0.resids, desc(.fitted)) %>%
select(2:5, p, warning) %>%
slice(1:10)
#> # A tibble: 10 x 6
#> ROS ROI debt_ratio .fitted p warning
#> <dbl> <dbl> <dbl> <dbl> <dbl> <lgl>
#> 1 - 25.0 -10071 452 860 1.00 T
#> 2 -292 - 17.9 0.0896 266 1.00 T
#> 3 - 96.0 - 176 0.0219 92.3 1.00 T
#> 4 - 25.4 - 548 6.43 49.5 1.00 T
#> 5 - 1.80 - 238 21.2 26.9 1.000 F
#> 6 - 5.65 - 344 11.3 26.6 1.000 F
#> 7 - 0.597 - 345 4.43 16.0 1.000 F
#> 8 - 2.62 - 359 0.444 15.0 1.000 F
#> 9 - 0.470 - 193 9.87 13.8 1.000 F
#> 10 - 2.46 - 176 3.64 9.50 1.000 F
So there are four observations that are causing the issue. They all have extreme values of one or more covariates.
But there are lots of other observations that are similarly close to 1.
There are some observations with high leverage -- what do they look like?
arrange(glm0.resids, desc(.hat)) %>%
select(2:4, .hat, p, warning) %>%
slice(1:10)
#> # A tibble: 10 x 6
#> ROS ROI debt_ratio .hat p warning
#> <dbl> <dbl> <dbl> <dbl> <dbl> <lgl>
#> 1 0.995 - 2.46 4.96 0.358 0.437 F
#> 2 -3.01 - 0.633 1.36 0.138 0.555 F
#> 3 -3.08 -14.6 0.0686 0.136 0.444 F
#> 4 -2.64 - 0.113 1.90 0.126 0.579 F
#> 5 -2.95 -13.9 0.773 0.112 0.561 F
#> 6 -0.0132 -14.9 3.12 0.0936 0.407 F
#> 7 -2.60 -10.9 0.856 0.0881 0.464 F
#> 8 -3.41 -26.4 1.12 0.0846 0.821 F
#> 9 -1.63 - 1.02 2.14 0.0746 0.413 F
#> 10 -0.146 -17.6 8.02 0.0644 0.984 F
None of those are problematic. Eliminate the four observations that trigger the warning; does the answer change?
ratios2 <- filter(ratios.complete, !glm0.resids$warning)
glm1<-glm(Default~ROS+ROI+debt_ratio,data=ratios2,family=binomial)
summary(glm1)
#>
#> Call:
#> glm(formula = Default ~ ROS + ROI + debt_ratio, family = binomial,
#> data = ratios2)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -2.8773 -0.3133 -0.2872 -0.2363 3.6160
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -3.75915 0.30621 -12.277 < 2e-16 ***
#> ROS -0.91929 0.24571 -3.741 0.000183 ***
#> ROI -0.04445 0.00898 -4.949 7.45e-07 ***
#> debt_ratio 0.86871 0.29135 2.982 0.002867 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 585.47 on 994 degrees of freedom
#> Residual deviance: 372.43 on 991 degrees of freedom
#> AIC: 380.43
#>
#> Number of Fisher Scoring iterations: 6
tidy(glm1)[,2] - tidy(glm0)[,2]
#> [1] 2.058958e-08 4.158585e-09 -1.119948e-11 -2.013056e-08
None of the coefficients changed by more than 10^-8! So essentially unchanged results. I'll go out on a limb here, but I think that's a "false positive" warning, nothing to worry about.
This warning arises with complete separation, but in that case I would expect to see the coefficient for one or more covariates get very large, with a standard error
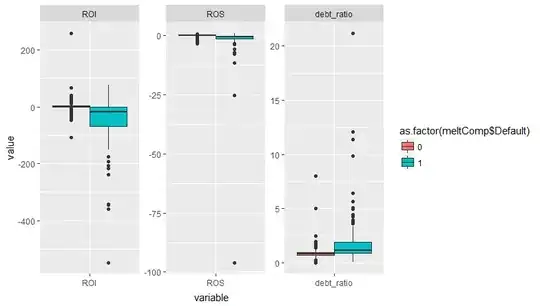
that is even larger. That's not occurring here, and from your plots you can see that the defaults occur across overlapping ranges of all covariates.
So the warning occurs because a few observations have very extreme values of the covariates. That could be a problem if those observations were also
highly influential. But they're not.
In the comments you asked "Why does standardization blow up the standard errors?". Standardizing your covariates changes the scale. The coefficients and standard errors
refer to a one unit change in the covariate, always. So if the variance of your covariate is larger than 1, then standardizing is going to shrink the scale.
A one unit change on the standardized scale is the same as a much larger change on the unstandardized scale. So the coefficients and standard errors will get larger. Look at the
z values -- they should not change even if you standardize. The z value of the intercept changes if you also center the covariates, because now it is estimating
a different point (at the mean of the covariates, instead of at 0)
ratios.complete2 <- mutate(ratios.complete,
scROS = (ROS - mean(ROS))/sd(ROS),
scROI = (ROI - mean(ROI))/sd(ROI),
scdebt_ratio = (debt_ratio - mean(debt_ratio))/sd(debt_ratio))
glm2<-glm(Default~scROS+scROI+scdebt_ratio,data=ratios.complete2,family=binomial)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# compare z values
tidy(glm2)[,4] - tidy(glm0)[,4]
#> [1] 4.203563e+00 8.881784e-16 1.776357e-15 -6.217249e-15
Created on 2018-03-25 by the reprex package (v0.2.0).