Directed acyclic graphs (DAGs) are efficient visual representations of qualitative causal assumptions in statistical models, but can they be used to present a regular instrument variable equation (or other equations)? If so, how? If not, why?
2 Answers
Yes.
For example in the DAG below, the instrumental variable $Z$ causes $X$, while the effect of $X$ on $O$ is confounded by unmeasured variable $U$.
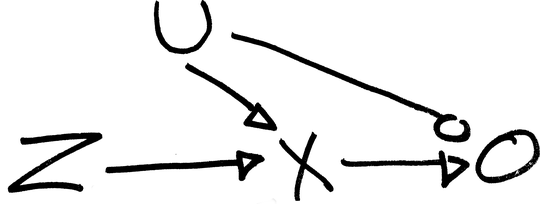
The instrumental variable model for this DAG would be to estimate the causal effect of $X$ on $O$ using $E(O|\widehat{X})$, where $\widehat{X} = E(X|Z)$.
This estimate is an unbiased causal estimate if:
$Z$ must be associated with $X$.
$Z$ must causally affect $O$ only through $X$
There must not be any prior causes of both $O$ and $Z$.
The effect of $X$ on $O$ must be homogeneous. This assumption/requirement has two forms, weak and strong:
- Weak homogeneity of the effect of $X$ on $O$: The effect of $X$ on $O$ does not vary by the levels of $Z$ (i.e. $Z$ cannot modify the effect of $X$ on $O$).
- Strong homogeneity of the effect of $X$ on $O$: The effect of $X$ on $O$ is constant across all individuals (or whatever your unit of analysis is).
The first three assumptions are represented in the DAG. However, the last assumption is not represented in the DAG.
Hernán, M. A. and Robins, J. M. (2020). Causal Inference. Chapter 16: Instrumental variable estimation. Chapman & Hall/CRC.
-
I think it would be helpful to replace $Y$ to $O$ for consistent notation. – dimitriy Mar 14 '18 at 21:21
-
Is (4) necessary for just ATE? I care about the ATE for compliers only, do I need it? – dimitriy Mar 14 '18 at 21:28
-
@DimitriyV.Masterov Thank you. Corrected $Y$ for $O$. I appreciate IV estimation, but am also a tad wary of it: playing around with reasonable values corresponding to the above assumptions shows that it is a frail method... often is not able to dispense with bias. As a consequence I would always try and simulate data from a model you think corresponds to your IV model, and then would see how well the IV estimation recovers your initial parameters. What does ATE mean? – Alexis Mar 14 '18 at 22:45
-
3ATE is average treatment effect, which is the effect for a randomly plucked person in the population. IV with a monotonicity assumption (or no defiers) recovers only the local average treatment effect for the people who comply with the assignment, which is typically different from the population ATE if there's any heterogeneity, but often more interesting from a policy perspective. – dimitriy Mar 14 '18 at 23:00
-
@DimitriyV.Masterov When is LATE of policy interest but not the ATE? – Julian Schuessler Mar 15 '18 at 14:45
-
@Alexis Note that weak homogeneity requires the effect of X on O conditional on X (!) not to vary with Z (this is explained in Hernan/Robins). Usually (always?), when Z is a valid instrument for X -> O, it cannot modify the effect of X on O, because Z does not influence O except through X. – Julian Schuessler Mar 15 '18 at 14:47
-
1@JulianSchuessler When the policy option consists of moving the instrument, the LATE/CATE is the right effect. For example, if the policy is a tax credit for solar panels, the impact for those who install only with the credit in place is the relevant one. For policy, we are often interested in the marginal entrant. – dimitriy Mar 15 '18 at 14:55
-
@CarlosCinelli I intended to write CACE (Complier Average Causal Effect), which I believe is equivalent to LATE. – dimitriy Mar 16 '18 at 18:00
-
1Why is it sufficient that Z is only associated with X (criterion 1)? Is it sufficient that Z does not causally affect X but is correlated with X through som unmeasured variable U? If so, why? – Elias Dec 18 '19 at 16:06
-
@AnonymousIGuess Because what we are trying to leverage in IVE is $Z$'s information about $X$: that does not rely on $Z$ causing $X$. For example, (and unlike in the simple DAG in my answer) Hernán and Robins give a case where $Z \to S$, $U\to S$, and $U \to X$: $Z$ carries information about $X$ in this causal world (fig. 16.3). – Alexis Dec 18 '19 at 17:59
-
1@Alexis Thanks. I checked fig 16.3, and, intuitively, I find that the instrument should be valid in this case (do they prove it? I haven't read the book). However, suppose there is an unmeasured confounder $V$ that affects $Z$ and $A$. Then $Z$ will still be correlated (associated) with $A$ - but will it be valid? No, according to Imbens (page 40, second key assumption, 2019): https://arxiv.org/pdf/1907.07271.pdf (also, see fig 9c-9d). The condition is, moreover, not testable, since we need a causal assumption to be able to say that $V$ is, in fact, not a potential confounder. – Elias Dec 18 '19 at 18:04
-
@AnonymousIGuess I would be happy to entertain an *argument* you would like to put forth, but am not going to take "go read this (unreviewed) article" as such an argument. I happen to be *quite* comfortable—based on my own work with simulation, and with my sense of the literature—with confounding relationships, such as $V \to Z$, $V \to U$, and $U \to X$, or even $V \to Z$ and $V \to X$ implying quite strongly that $Z$ carries information about $X$. Of course, IVE is pretty frail, and, as with *all* observational causal inferences, relies on untestable assumptions. – Alexis Dec 18 '19 at 18:10
-
@AnonymousIGuess Thinking more: are you positing something like $V \to Z$, $V \to U$, $U \to Z$, and $U \to X$? – Alexis Dec 18 '19 at 18:14
-
1@Alexis I note that even though the article is unreviewed, Imbens is a world-renowned econometrician and an expert in the field. I wanted to refer to an accessible article and argument. His view is also expressed in standard, modern textbooks in causal inference in econometrics, such as "Causal Inference for Statistics, Social, and Biomedical Sciences". I am positing $V\to Z$ and $V\to A$ here, in addition to the causal relations expressed in fig. 16.3. One may also consider $V\to U$ and $U\to A$. I'm not positing $U\to Z$, though it may be considered. I'd guess one needs to control for $V$. – Elias Dec 18 '19 at 18:17
-
Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/102342/discussion-between-alexis-and-anonymousiguess). – Alexis Dec 18 '19 at 18:19
-
@Elias "My argument boils down to the statement that one can generate a causal system satisfying i-iii in the book, but where the IV-estimator does not pin down the true, causal effect." I (and the authors) have found that even when conditions i–iv are met, that IVR is a frail causal estimator. For example "weak instrument" is poorly defined. The authors point out that (1) IVR requires modeling assumptions even with $N=\infty$, (2) large biases can result from tiny deviations from i–iv, (3) IVR is strongest under simple DAGs with binary $X$. – Alexis Jan 04 '20 at 19:08
-
@Elias... I haven't yet got a chance to play with sims, but still look forward to doing so, and thank you for your illuminating discussion and reveal about Imbens. – Alexis Jan 04 '20 at 19:09
-
@Elias WRT the need for a causal association between $Z$ and $X$, I think there's also concern about selection bias *a la* $Z\to [V]$ and $X \to [V]$ where $[V]$ is inducing selection bias between $Z$ and $X$. (I have made an edit to my answer in light of our exchange.) – Alexis Jan 04 '20 at 19:29
Yes, they surely can.
As a matter of fact, the SCM/DAG literature has been working on generalized notions of instrumental variables, you might want to check Brito and Pearl, or Chen, Kumor and Bareinboim.
The basic IV dag is usually represented as:
Where $U$ is unobserved and $Z$ is an instrument for the effect of $X$ on $Y$. Although this is the graph you usually see, there are several different structures that would render $Z$ an instrument. For the basic case, to check whether $Z$ is an instrument for the causal effect of $X$ on $Y$ conditional on a set of covariates $S$, you have two simple graphical conditions:
- $(Z \not\perp X|S)_{G}$
- $(Z\perp Y|S)_{G_{\overline{X}}}$
The first condition requires $Z$ to be connected to $X$ in the original DAG. The second condition requires $Z$ to not be connected to $Y$ if we intervene on $X$ (represented by the DAG $G_{\overline{X}}$, where you remove the arrows pointing to $X$). You might want to check Causality (page. 248).
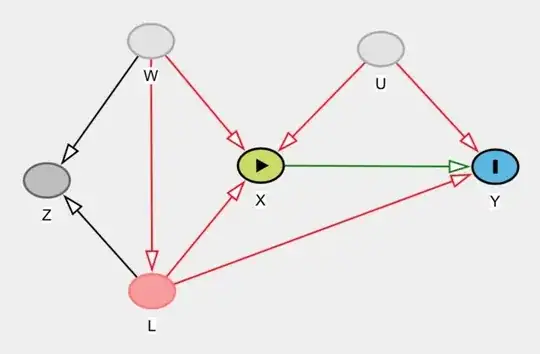
For example, consider the graph below, with $W$ and $U$ unobserved. Here, $Z$ is, conditional on $L$,an instrument for the causal effect of $X$ on $Y$. We can create more complicated cases where it might not be immediately obvious whether something does qualify as an instrument or not.
One final thing you should have in mind is that identification using instrumental variable methods needs parametric assumptions. That is, finding an instrument is not enough for identification of the effect: you need to impose parametric assumptions, such as linearity or monotonicity and so on.
- 10,500
- 5
- 42
- 77
-
-
1@DimitriyV.Masterov what is the $A1$ you are referring to? Is it $(Z \not\perp X|L)_{G}$? That holds because $W$ is a common cause of $Z$ and $X$. – Carlos Cinelli Mar 15 '18 at 01:27