4

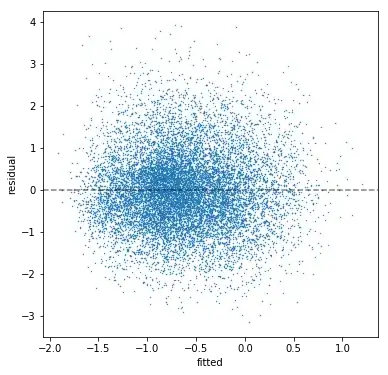
I'm working in Python with statsmodels. I estimate a multiple regression model (n=10763; 12 predictors; r^2=0.216; all coefficients have signs pointing the correct direction and are significant). Then I check my residuals. The residuals show no discernible pattern, so there appears to be negligible heteroskedasticity:

residuals vs fitted

The residuals have a Jarque-Bera test statistic of 338.7 with a p-value of 2e-75. The skew is 0.317 and the kurtosis is 3.543. We can see this in a histogram of the residuals:

residuals histogram

And in the residuals' q-q plot:

residuals q-q plot

I have two questions, relating to satisfying the OLS assumption that the residuals have a normal distribution to get meaningful p-values.

The first is how to interpret if your residuals are "close enough" to normally distributed. Presumably, a sufficiently large sample size will always fail the J-B test and other related tests -- i.e., producing a p-value below .05 so we can reject the null hypothesis that the residuals are normally distributed. But looking at the histogram and the q-q plot, how close to "perfect" do we expect them to be? They seem to show the thin tails and slight right skew. Given real-world data, what is "good enough"?

Second question: what sort of model re-specifications or corrections would one typically explore to correct for residuals distributed with high kurtosis?

eos
  • 323
  • 4
  • 13
  • 2
    Why do you care? Close enough to Normal for what purpose? – jbowman Mar 08 '18 at 19:06
  • @jbowman to satisfy the OLS assumption that the residuals have a normal distribution. – eos Mar 08 '18 at 19:08
  • 4
    OLS doesn't actually require Normality; it minimizes the sum of the squared errors of the model regardless of what the underlying distributional assumptions are. If we assume the residuals ~ Normal, then we get the nice Normal distribution of the parameters, but with lots of data (as you have) and not-too-horrible true distributions (and yours aren't bad), you'll have a Central Limit Theorem effect take over and can make inferences about the parameters without having to mess about with the residuals or reformulating the model. (I know this doesn't answer your broader question, though.) – jbowman Mar 08 '18 at 19:14
  • @jbowman the residuals are assumed to be asymptotically normal to get meaningful t-stats and p-values for hypothesis testing, no? Is your point that a sufficiently large sample and an "ok" distribution will overcome the limitations of non-normally distributed residuals? If so, I'm wondering how to determine what "ok" means. – eos Mar 08 '18 at 19:21
  • 2
    No, the residuals aren't what's assumed to be asymptotically normal (since they are assumed i.i.d., their asymptotic distribution is the same as the distribution of, let us say, the very first one.) Think of it as if it were the sample mean; the dist'n of the sample mean is what needs to be asymptotically normal for t-tests to work (with large enough sample sizes, which are often quite small,) not the dist'n of the individual $x_i$. You have grasped my point correctly, but answering the question will require much more than a comment. – jbowman Mar 08 '18 at 19:26
  • 3
    See https://stats.stackexchange.com/search?q=normality+tests+useless for extensive commentary on these issues. – whuber Mar 08 '18 at 19:57

1 Answers1

2

What's "close enough" is application specific. For instance, when estimating the regression parameters, the residual distribution doesn't need to be normal, it can be anything, pretty much. When estimating the variance (uncertainty) of regression parameters, the residual distribution doesn't need to be normal, but it helps when it is. In this case, asymptotically due to central limit theorem, in most cases you'll get a good estimate of the variance with almost any distribution too as long as the variance is finite.

However, there will be some applications where the distribution has to be normal. For instance, suppose you're managing a risk of a business using value-at-risk approach. In this case, you make forecast of a revenue or a value of a business for the next period, maybe next day. Then you build the distribution of outcomes: $\hat y_{t+1}=X_{t+1}\beta_{t+1}+\varepsilon_{t+1}$ The value-at-risk is $\alpha$-quantile of $\hat y_{t+1}$, which depends on the distribution of $\varepsilon_{t+1}$. If you assume the distribution to be normal and it's not, then you can underestimate the risk.

This happened on a massive scale during the last recession when almost everyone understimated the risk from certain derivatives assuming that the distribution was normal instead of actual (unknown) fatter tailed distribution. This contributed to the severity of the last recession to some degree.

Aksakal
  • 55,939
  • 5
  • 90
  • 176