When I run a regression with an interaction term (composed of one continuous variable and one binary variable) and several covariates, I get an interaction term value of -6.52. However, when I run two separate regressions for each value of the binary variable, the coefficients of the predictors are not -6.52 apart. This only occurs when I include the covariates in the model, does anyone know why?
1 Answers
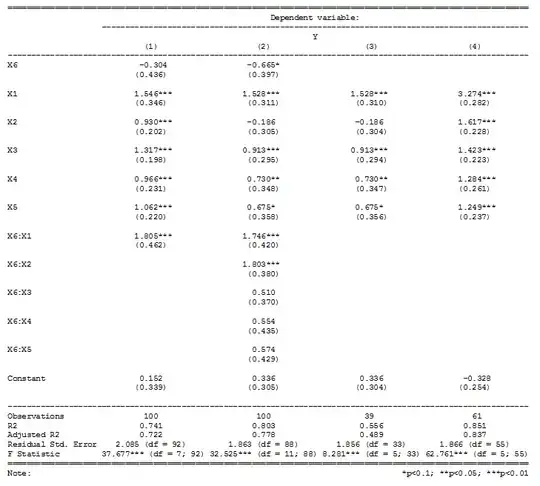
Separate regressions is equivalent to the interaction of all of your covariates and the binary variable. From your description, it sounds like you only fitted the interaction of one of the covariates and the binary variable. See the simulated data below.
set.seed(20180216)
sim_data <- data.frame(matrix(c(rnorm(500), rbinom(100,1,.5) ) , 100,6) )
sim_data$Y <- with( sim_data, X1 + X2 + X3 + X4 + X5 + 2 * X1 * X6 ) + rnorm( 100, 0, 2 )
model1 <- lm( Y ~ X6 * X1 + X2 + X3 + X4 + X5 , data = sim_data )
model2 <- lm( Y ~ X6 * (X1 + X2 + X3 + X4 + X5) , data = sim_data )
model3 <- lm( Y ~ X1 + X2 + X3 + X4 + X5 , data = sim_data , subset = sim_data$X6==0 )
model4 <- lm( Y ~ X1 + X2 + X3 + X4 + X5 , data = sim_data , subset = sim_data$X6==1 )
library(stargazer)
stargazer(model1,model2, model3, model4, type="text")
Model 1 in the image is the model you fitted which shows the interaction of X1 and the binary X6. Model 2 fits the model with the interaction of X6 and all 5 of the other covariates. Models 3 and 4 fit the separate regressions by group 0 and 1 respectively.
Immediately you will notice that the coefficients for model 3 are the same as those for the main effects of X1-X5 in model 2.
The coefficients for model 4 are the sum of the model 2 coefficients:
- X1 + X1 * X6
- X2 + X2 * X6
- ...
- X5 + X5 * X6
The term for X6 in model 2 is the difference in the slopes in models 3 & 4.
- 5,708
- 3
- 29
- 41
-
Is it incorrect to only fit the interaction of one of the covariates and the binary variable? Should I instead use the interactions of the binary variable with all of the covariates? – Benji Feb 20 '18 at 19:22
-
1It is not incorrect. It depends on the hypothesis that you wish to test and the assumptions you are willing to make. If you are only interested in the single interaction and are willing to assume that the coefficients for your other covariates are the same across groups, then your approach is fine. It is just different than separate regressions. – Brett Feb 20 '18 at 19:36
-
I am only interested in the single interaction, but if I am not willing to assume that the other covariates are the same across the binary variable groups, the safer approach is to take the interactions of all the covariates with the binary variable? – Benji Feb 20 '18 at 19:45
-
1That's correct. Which is exactly the same as fitting separate regression (which has the advantage that it is, in my opinion, more straight forward to interpret). A great set of notes here to put some language around this: https://www3.nd.edu/~rwilliam/stats2/l52.pdf – Brett Feb 20 '18 at 19:49
-
Exactly the same except that using the moderation model will tell you whether the difference between groups is significant, right? Or is there a better way to compare them? – Benji Feb 20 '18 at 20:27
-
1True. Also valuable the discussion here on testing coefficients across models: https://stats.stackexchange.com/q/13112/485 – Brett Feb 20 '18 at 21:23