7

I have ran a simple regression with a continuous response variable and a categorical explanatory variable (with 2 levels). I am currently checking that the model meets the assumptions of regression. I produced the following plot:

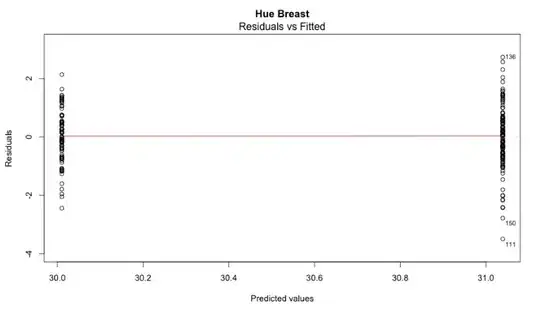
enter image description here

I'm aware that I need to check that the residuals are normally distributed. Do I need to check the distribution of residuals at each of the 2 levels of the explanatory variable? Or do I need to check the distribution of all residuals simultaneously?

Community
  • 1
luciano
  • 12,197
  • 30
  • 87
  • 119

1 Answers1

7

(Note that a regression model with only 1 explanatory variable that is categorical and has just 2 levels is equivalent to a t-test; there's nothing wrong with calling it a regression, but it would most commonly be discussed / referred to as a t-test.)

You check the distribution of all the residuals simultaneously. There are tests for normality, but I'm not a huge fan of them (I listed some in my answer to your previous question). I think the best option is to make a qq-plot. You can find a really nice version (qq.plot) in John Fox's car package. Among other features, it'll give you a 95% confidence band, which can help you interpret the plot.

On a different note, from looking at your plot, I don't know if you have more data in the second group, but you should also check to ensure you have homogeneity of variance.

Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • Of course testing homogeneity of variance means comparin gthe sample variances of the two groups. I agree with gung's answer completely. – Michael R. Chernick Jul 21 '12 at 14:01
  • @gung, you don't need homogeneity of variance to do a two sample $t$-test, do you? – Macro Jul 21 '12 at 16:20
  • @Macro, if you don't have equality of variance then you should use the [Satterthwaite-Welch](http://en.wikipedia.org/wiki/Welch%E2%80%93Satterthwaite_equation) correction for the degrees of freedom of the [t-test](http://en.wikipedia.org/wiki/Welch%27s_t_test). – gung - Reinstate Monica Jul 21 '12 at 16:37
  • @gung, so, in this special case of regression, lack of homogeneity of variance is an easily remedied problem (+1,btw). – Macro Jul 21 '12 at 17:12
  • It is possible that checking the pooled residuals will give the wrong impression. The correctly stated assumption is that the conditional distributions of Y are normal for all X. It is possible that all conditional distributions are non-normal, yet the combined distribution of the residuals is close to (or even exactly) normal. One example occurs with ordinal Y (say 1,2,3,4,5): the pooled residuals are continuous-looking, may pass the normality tests, and may have q-q plots that appear perfectly normal. Yet obviously normality is violated because of discreteness. – BigBendRegion Oct 25 '18 at 18:28