I'm faced with analyzing the following design:
In a longitudinal study, the muscle tissue of about 25 subjects are analyzed at 8 timepoints. Specifically, 7 measurements are taken during a race during multiple days (I don't know the spacing of the measurements). The 8th measurement is several weeks after the race. At each time point, muscle measurements in 4 separate muscle groups in both legs (left and right) are assessed. There is one observation per subject/leg/muscle group/time point. As I see it, this is a crossed design, because both legs and all muscle groups are analyzed for each participant.
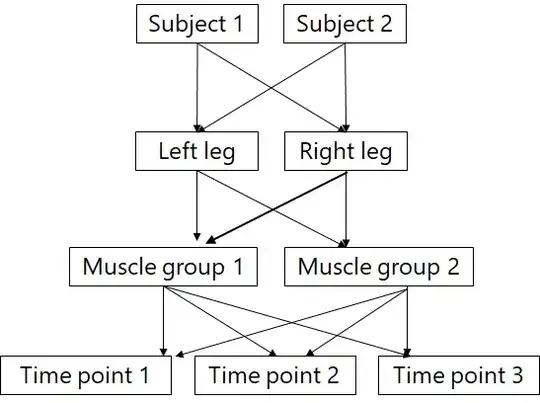
I have tried to graphically summarize the (simplified) design (just for 2 subjects and 2 muscle groups for simplicity):
Information about the model:
- Time points will be treated categorically and not continuously.
- Fixed effects will include time point (categorical), age (continuous), sex (cateogrical), leg (categorical), muscle group (cateogrical) and another muscle parameter (continuous).
- Random effects will at minimum include a random intercept per subject (i.e.
(1 | subject)inlmer). - The goal is i) assess the relationship between the outcome and the other muscle parameter that is also measured at each time point.
My questions:
- What are possible/sensible random effects for such a study design?
- What are the "maximal" random effects for this study design?
I'm using lmer from the lme4 package in R and would appreciate suggestions in this regard (also the software is not crucial).