2

I have two continuous distributions and I am trying to compare them using KS test using R Studio with the code below:

f1 <- "filename1"
f2 <- "filename2"

readDataFromCSV <- function(filename) {
  packetsData <- read.csv(file=filename, header=TRUE, sep=",")
  return(packetsData)
}

pd1 <- readDataFromCSV(f1) // x
pd2 <- readDataFromCSV(f2) // y

timecdf1 <- ecdf(pd1$Time)
timecdf2 <- ecdf(pd2$Time)

colors37 = c("red","blue","brown","orange","black","purple", "green","cyan", "navy", "pink", "maroon", "grey", "black", "coral", "lavender", "magenta", "yellow", "azure", "bisque", "darkcyan")
ksResult <- ks.test(pd1$Time, pd2$Time, alternative = "greater")
print(ksResult)


plot(timecdf1, verticals=TRUE, do.points=FALSE, col=colors37[1], ylab = '', xlab='Time(sec)');par(new=TRUE)
plot(timecdf2, verticals=TRUE, do.points=FALSE, add=TRUE,col=colors37[5])

When I apply the KS test it results in the following:

    Two-sample Kolmogorov-Smirnov test

data:  pd1$Time and pd2$Time
D^+ = 0.015708, p-value = 0.9213
alternative hypothesis: the CDF of x lies above that of y

And when I draw the ecdfs of the values the results are shown below: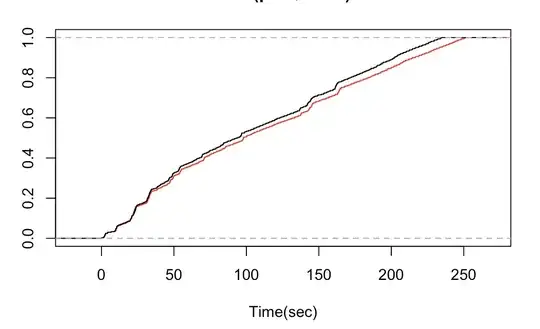enter image description here

The 'x' represents the red line on the graph and 'y' represents the black line. I don't understand why the graph shows x below the y. On the other hand KS test of the x and y shows a high value of p indicating that x should lie above y.

I am missing something trivial in interpretation of the KS test.

Hassan Abbas
  • 121
  • 4
  • I can't see your data and your graph doesn't label x and y. but I think I see your problem. **The variable with generally higher values will have lower cumulative probability at any given value.** Compare the heights of basketball players (taller than average) and jockeys (shorter). The basketball players are likely to have a cumulative probability near zero for heights like 1.8 m and the jockeys a cumulative probability near one for the same heights. – Nick Cox Jan 18 '18 at 10:41
  • This is one reason why quantile plots (axes reversed as compared with your plot) are preferable (in my view) to plots of the cumulative distribution function. The groups with higher values ... plot higher on the graph in quantile plots. – Nick Cox Jan 18 '18 at 10:42
  • @NickCox, the axis are labelled correctly i think for the ecdf, x axis is labelled correctly for the Time in seconds, where as y axis is not labelled since its a default ecdf. However, legends are not added which should be the case. The x is the red line and y is the black line on the graph. Is there any solution to this problem, and i need to justify why i need to reverse the graph ? – Hassan Abbas Jan 18 '18 at 10:49
  • My point was that we didn't know which was x (red) and which y (black) until you just told us. The plot of ecdfs is relevant to Kolmogorov-Smirnov; it's just oversold compared with quantile plots, which show the same information but are often more effective. That thread answers a different question, but the references are all excellent. – Nick Cox Jan 18 '18 at 11:14
  • The thread alluded to above is https://stats.stackexchange.com/questions/64026/benefits-of-using-qq-plots-over-histograms – Nick Cox Jan 18 '18 at 12:34
  • You appear to misinterpret p: a large p-value indicates **no** significant difference was found between the distributions. – whuber Jan 18 '18 at 16:05
  • @whuber, Well if the test is two sided as in the statement ksResult – Hassan Abbas Jan 18 '18 at 17:54
  • 2
    The p value is high because there's little difference between the two. You seem to be confusing a symmetric two-tailed test with the two forms of the KS test. The KS statistic for the two-tailed test is the *larger* of the two unidirectional KS statistics. Its p-value is not merely a doubling of the p-value of a unidirectional result. – whuber Jan 18 '18 at 19:12
  • One can easily see why it should not be double -- because the two one-sided cases are not mutually exclusive -- the same sample could generate a difference in both directions (sitting both above in one place and below in another) – Glen_b Jan 19 '18 at 00:27

0 Answers0