Suppose we have 2 classes. By using naive Bayes classifier we get posterior probabilities P(C1|D) and P(C2|D) for query sample.....suppose P(C1|D) is higher than P(C2|D), then we assign the tag of class 1 to query sample.
My question is this :
Where does the threshold come into picture here and why and how do we use 5-fold cross validated accuracy to find the ideal threshold for Naive Bayes algorithm??
In short: The threshold is not a part of the Naive Bayes algorithm
A Naive Bayes algorithm will be able to say for a certain sample, that the probability of it being of C1 is 60% and of C2 is 40%. Then it's up to you to interpret this as a classification in class C1, which would be the case for a 50% threshold. When using accuracy as a metric you essentially count the amount of correct classifications and thus state a definite threshold (like 50%) that is used to determine which class is being predicted for each sample.
You might want to take a look at this answer, and Frank Harrell's Classification vs. Prediction.
Why cross validation? Because you want to use a separate training/test set and use all your data. How? You could determine recall & precision for every fold and every threshold and make a choice.
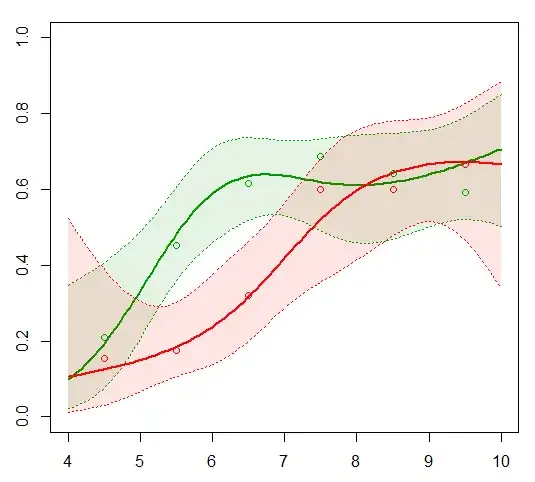
Some sidenote: Naive Bayes has the tendency to push probabilities to extremes (0% and 100%), it's what they call badly calibrated. It's due its basic assumption that all attributes are conditionally independent which is often not the case. The latter is visible in the example below; some metrics are plotted in function of threshold for a Naive Bayes classifier on a spam task.
