Different results for between/within groups and within group regression analyses

Question

I have a lmer model that analyse the interaction between a treatment (4 levels. Name: Relation_PenultimateLast) and 3 groups (ExpertiseType), crossed. In this model I have 3 by-group random effects.

The function used is lmer from the library lme4, extended through the lmerTest library.

Here the formula:

f.e.model = lmer(Score ~ Relation_PenultimateLast*ExpertiseType + (1|TrajectoryType) + (1|StimulusType) + (1|LastPosition), data=datasheet.complete)

Results:

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.43700 -0.87535 -0.03117  0.76091  2.06034 

Random effects:
 Groups         Name        Variance Std.Dev.
 TrajectoryType (Intercept) 0.019520 0.13971 
 LastPosition   (Intercept) 0.008778 0.09369 
 StimulusType   (Intercept) 0.028348 0.16837 
 Residual                   1.292387 1.13683 
Number of obs: 8200, groups:  
TrajectoryType, 25; LastPosition, 8; StimulusType, 4

Fixed effects:
                                         Estimate Std. Error         df t value
(Intercept)                               3.34934    0.13401   17.00000  24.993
Relation_PenultimateLast                 -0.08738    0.03453   77.00000  -2.531
ExpertiseType                            -0.09808    0.03639 8165.00000  -2.695
Relation_PenultimateLast:ExpertiseType    0.05224    0.01271 8165.00000   4.110
                                       Pr(>|t|)    
(Intercept)                            7.55e-15 ***
Relation_PenultimateLast                0.01343 *  
ExpertiseType                           0.00705 ** 
Relation_PenultimateLast:ExpertiseType 3.99e-05 ***

Using the plot function:

f.e.model.plot = datasheet.complete
f.e.model.plot$fit <- predict(f.e.model)
interaction.plot(x.factor = f.e.model.plot$Relation_PenultimateLast, trace.factor = f.e.model.plot$ExpertiseType, 
                 response = f.e.model.plot$fit, fun = mean, 
                 type = "b", legend = TRUE,
                 fixed=TRUE,
                 xlab = "Penultimate_Last category", ylab="Cadential effectiveness", trace.label = "Expertise",
         pch=c(1,19), col = c("#00AFBB", "#E7B800", "#FF0000")
)

I obtain this graph:

Note the yellow line, ParticipantType = 2

I would expect the yellow line to represent the effects of the treatment within the group 2, but if I run the same analysis mode within the group:

datasheet.complete.performers = subset(datasheet.complete, ExpertiseType==2)   #create a subset with only composers
f.e.model.performers = lmer(Score ~ Relation_PenultimateLast + (1|TrajectoryType) + (1|StimulusType) + (1|LastPosition), data=datasheet.complete.performers)

Results:

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.41905 -0.87678  0.02313  0.76503  1.85794 

Random effects:
 Groups         Name        Variance Std.Dev.
 TrajectoryType (Intercept) 0.01906  0.1381  
 LastPosition   (Intercept) 0.01179  0.1086  
 StimulusType   (Intercept) 0.06358  0.2522  
 Residual                   1.39162  1.1797  
Number of obs: 2400, groups:  
TrajectoryType, 25; LastPosition, 8; StimulusType, 4

Fixed effects:
                         Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)               3.40381    0.15825  6.70100  21.509 1.96e-07 ***
Relation_PenultimateLast -0.03909    0.03059 23.09500  -1.278    0.214 

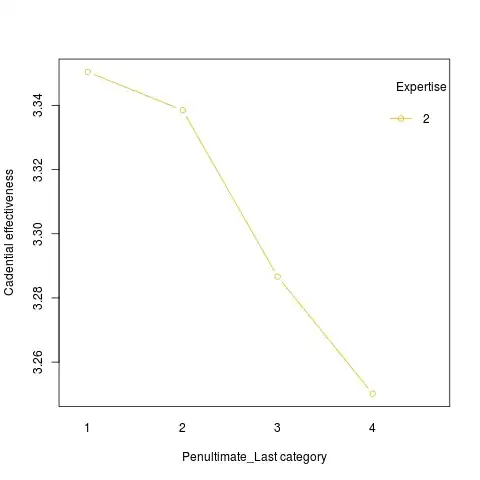
I obtain a complete different scenario:

f.e.model.performers.plot = datasheet.complete.performers
f.e.model.performers.plot$fit <- predict(f.e.model.performers)
interaction.plot(x.factor = f.e.model.performers.plot$Relation_PenultimateLast, trace.factor = f.e.model.performers.plot$ExpertiseType, 
                 response = f.e.model.performers.plot$fit, fun = mean, 
                 type = "b", legend = TRUE,
                 fixed=TRUE,
                 xlab = "Penultimate_Last category", ylab="Cadential effectiveness", trace.label = "Expertise",
                 pch=c(1,19), col = c("#E7B800"))

Should not the two representation of the effect of Relation_PenultimateLast be the same? Should I consider the second graph the correct representation? Or should this be a warning that there is still some random effect that is not counted in the formula?

Answer 1

By only using one group, you're changing the amount of pooling going on, which affects shrinkage and the bias-variance / over- vs. underfitting tradeoff. When you fit a model to a subset, it will generally be better at describing that subset but often worse at describing the full set / other sets. In other words, your subset model better describes the subset because it doesn't have to spend "resources" describing the other data, but of course this also means that it will tend to not describe the other data as well - it's better at the small details but worse at the big picture.

On a somewhat different note, you're treating your variables as continuous predictors and not as categorical (in the mixed model -- this is apparent in the summary; your plots are more agnostic about whether the predictors are categorical or continuous). Whether or not this is the correct modelling choice depends on many things, but make sure it's what you want! Without further information, it may be reasonable to treat expertise as a continuous even if it is "only" ordinal, but "category" sounds like something that may not be properly modelled by a continuous variable.