How to simulate anomalous diffusion of a 1D point like particle?

Question

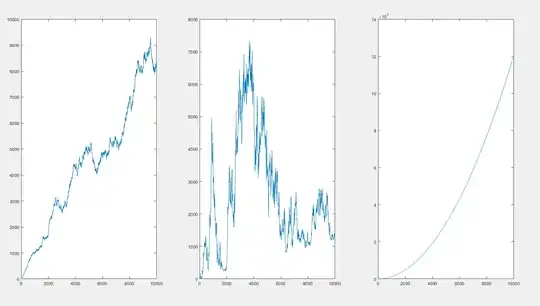
I want to simulate 3 types of diffusion processes:

1. normal diffusion $[\langle x^2(t)\rangle \propto t ]$.
2. subdiffusion $[\langle x^2(t)\rangle \propto t^\alpha ; \alpha<1 ]$
3. superdiffusion $[\langle x^2(t)\rangle \propto t^\alpha ; \alpha>1]$

I was trying to do the following:

close all
M=1e4;
N=50;
dx=randn(M,N);

sub = dx;
sup = dx;
alpha=0.8;
for i =2:M
    for j=1:N
        if rand > 0.1
            center = (1-alpha) * sub(i,j) + alpha * sub(i-1,1);
            sub(i,j) = mean(random('norm',center,0.1,1,5));
            center = alpha * sup(i,j) + (1-alpha) * sup(i-1,1);
            sup(i,j) = random('norm',1+center,1,1,1);
        end
    end
end


x=cumsum(dx);
xSub=cumsum(sub);
xSup=cumsum(sup);

MSD_x=mean(x.^2,2);
MSD_xSub=mean(xSub.^2,2);
MSD_xSup=mean(xSup.^2,2);

ND = loglog(0:M-1,MSD_x);
hold on
SUB = loglog(0:M-1,MSD_xSub);
SUP = loglog(0:M-1,MSD_xSup);

fit(ND.XData',ND.YData', 'poly1')
fit(SUB.XData',SUB.YData', 'poly1')
fit(SUP.XData',SUP.YData', 'poly1')
figure
subplot(1,3,1)
plot(0:M-1, MSD_x)
subplot(1,3,2)
plot(0:M-1, MSD_xSub)
subplot(1,3,3)
plot(0:M-1, MSD_xSup)

The MSD as function of time:

Here is the loglog scale of the 3 signals:

Why don't I get the right profiles as in the first figure?