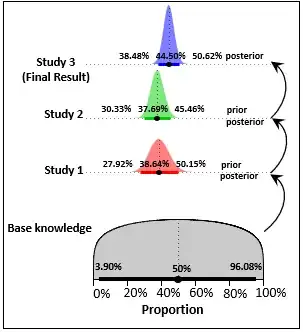
"Yesterday’s posterior is today’s prior" is the best Bayesian learning strategy if you know with absolute certainty that "Today's parameter is yesterday's parameter".
is it possible to use a wide prior for the oldest study, and then use
its posterior as prior for the study after it and so on to arrive at
one final posterior for the most recent study?
Yes as long as you know you are making inferences about the same (unknown) parameter:
- same model
- same experimental conditions (including sampling from the same population)
- no deviation due to time depending or local phenomena
Note that if the lines in each dataset are considered to be independent of each other, the final posterior you get is the same as when considering all studies as a whole: merging all datasets into one (just basic copy/paste).
An interesting case in which such a simplifying assumption may hold or not is the Kalman Filter (or more generally Bayes filters): you acquire information at each observation making the prior dynamically evolve as $prior_{t+1}=posterior_t$.
But if at the same time, some random process is disturbing the parameter (known as "state" in Kalman filters), then the prior must be updated too due to this process. Your prior narrows down at each observation, but between two observations it broadens due to random changes.
In that case the prior you would use in the next study would be a broadened version of the posterior of the previous study. How much depends on the random dynamics and is very complicated, thus rarely done in practice.