i try to find an algorithm that meets my expectations.
Following Scenario: I want to predict the delivery of natural ressources (ores). So i have data with composition of the ressources from a delivery (with date and supplier). Now i want to predict the composition of the ressources, that the supplier x will send me at date y.
You can see the composition as a vector A = {a1,a2,a3,a4,a5}. a1 represents the occur of a material in percent in A. So A sums up to 100%. a1 depends on the old data and a2,a3,a4 and a5.
So i have the input X and Y and want to predict the vector A. Wich algorithm should i use to train my model? Is there any algorithm to predict A with X and Y as input and the old deliveries?
I was thinking of multivariante regression, but i need multiple outputs too and dependences between a1,a2,a3,a4 and a5.
I`m looking forward to your ideas!
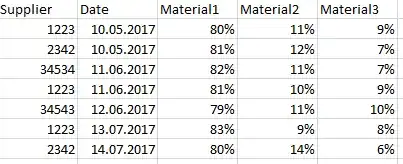
Edit: The structure of the data looks like (These are dummy data, but very close to the real one. The dummy data have the same temporal evolution as the real data) :
As you can see there different supplier. The same supplier id means that the ressource is form the same location. Because of this the input should be the date of delivery and the supplier.
Note: I only want to predict deliveries from current suppliers (that means i have data about the composition from older deliveries). I do not want to predict the composition of a delivery from a new supplier. These are all long-term-suppliers, so i have data from the last 10 years. The amount of a material in a delivery fluctuates (because the ore vein is not solid block), but is always in the same are (for example material 1 is always between 75% and 85%).