3

I'm trying to find out if my data are fitting a t-distribution. My data set is very large (more than 5000 data) and I used "fitdistr" (MASS package) to estimate mean, sd and df. I used the Kolmogorov-Smirnov test ("ks.test.t", LambertW package in R) to asses the goodness of fit, but I read that it should not be used if the parameters of my distribution have been estimated from the sample.

First of all I was wondering why KS test should not work fine.

Is there a test, in R, to asses the goodness of fit with estimated parameters ? I'm really a beginner in using R, so I would appreciate if you can explain me step by step how to do it.

Thank you in advance! =)

Marco
  • 31
  • 3
  • Is there any problem applying the standard $\chi^2$ goodness-of-fit test? (If that's new to you, I have given a detailed explanation at https://stats.stackexchange.com/questions/16921/how-to-understand-degrees-of-freedom/17148#17148.) For information about the problems with using the KS test on fitted values, see https://stats.stackexchange.com/search?q=ks+test+fit+lilliefors. – whuber Nov 23 '17 at 14:18
  • The second paragraph of the "Description" section of the help on `ks.test.t` is quite explicit: "For estimated parameters of the t-distribution the p-values are incorrect and should be adjusted. See ks.test and the references therein (Durbin (1973)). As a more practical approach consider bootstrapping and estimating the p-value empirically." -- did you not check the help?? – Glen_b Nov 24 '17 at 03:03
  • @whuber , thank you for your answer, but I find difficult to understand how to adapt the R code given in your answer to a t distribution with estimated value. – Marco Nov 24 '17 at 10:06
  • 1
    @Glen_b Of course I read the help guide , but I didn't find any practical example about the application of those tests to the t distribution with estimated values. – Marco Nov 24 '17 at 10:14

1 Answers1

1

The Kolmogorov-Smirnov test is designed for situations where a continuous distribution is fully specified under the null hypothesis.

Let's look at what happens with the null distribution of the test statistic when the null hypothesis is true.

When you estimate parameters, the estimation identifies parameters that make the estimated distribution closer to the data than the population distribution is.

Let's take the slightly simpler example; the normal.

Here I generate a sample of 100 values from a $N(50,5)$ (the black points in the ECDF) and compare to the population distribution function (in blue) and the fitted distribution function (normal with the mean and variance set to the sample mean and variance, shown in red):

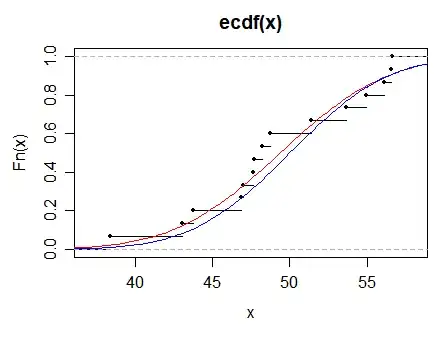
ECDF of a sample of size 15 from a normal distribution, with population cdf and fitted normal cdf

KS statistic for population parameters: D = 0.19987  
KS statistic for fitted distribution:   D = 0.14715

This it typical. However, it is possible for the statistic to be larger on the fitted because we don't actually fit the distribution by minimizing the KS statistic; if we did estimate parameters that way the fitted normal distribution would be guaranteed to have a smaller test statistic.

This "fitted is closer to the data than the population" is the same thing that results in dividing by $n-1$ in sample variance (Bessel-correction); here it makes the test statistic typically smaller than it should be.

So if you stuck with the usual tables the type I error rate would be smaller than you chose it to be (with corresponding lowering of power); your test doesn't behave the way you want it to.

You may like to read about Lilliefors test (on which there are many posts here). Lilliefors computed (via simulation) the distribution of a Kolmogorov-Smirnov statistic on fitted distributions under normal (unknown $\mu$, unknown $\sigma$, and both parameters unknown) and exponential cases (1967,1969)

Once you fit a distribution, the test is no longer distribution-free.

In the case where you're fitting the degrees of freedom parameter, I don't think Lilliefors approach will work for the t-distibution*; the advice to use bootstrapping may be reasonable in large samples.

* because the distribution of the test statistic will be different for different df (however, it might be that it doesn't vary much with df in which case you could still have a reasonable approximate test)

Glen_b
  • 257,508
  • 32
  • 553
  • 939