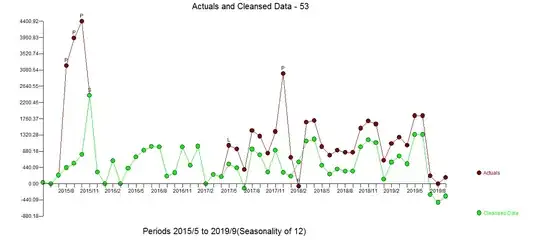
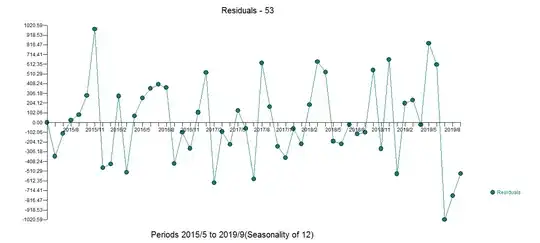
I trying to create a very simple forecasting routine for a time series. I am using three methods to fit and compare their accuracies. These methods are ets, auto.arima and stlf from forecast package. An example of a time series is shown below.
count <- c(231.61, 0.00, 228.70, 3197.99, 3941.62, 4400.92, 2386.03,
311.22, 0.00, 621.96, 0.00, 414.33, 719.38, 907.70, 1005.59, 998.46,
199.00, 298.35, 994.50, 497.01, 1013.48, 0.00, 249.86, 187.95, 1033.74,
939.77, 382.32, 1441.69, 1284.46, 823.41, 1410.24, 2976.88, 711.86, -74.90,
1661.38, 1712.29, 1000.45, 769.57, 904.88, 846.33, 846.33, 1501.34,
1696.61, 1615.40, 630.88, 1090.95, 1256.66, 1043.50, 1838.87, 1838.85,
212.39, 0.00, 171.31)
d.ts <- ts(count, start = c(2015, 5), freq = 12)
And, here are how I am doing every fitting.
library(forecast)
fit.ets <- ets(d.ts)
fit.stl <- stlf(d.ts, robust = T, s.window = "periodic")
fit.arima <- auto.arima(d.ts, stepwise = F, approximation = F)
When I try to plot the fitted values and original values, I get the following plot. Plotting fitted vs. original values
plot(fit.ets$x, col = "red")
lines(fitted(fit.ets), col = "blue")
It looks like as if there is a 1-lag between the original and fitted values. Plotting auto.arima fit
plot(fit.arima$x, col = "red")
lines(fitted(fit.arima), col = "blue")
produces similar results.
 Is this a normal behaviour? If it is, what is the cause?
Is this a normal behaviour? If it is, what is the cause?