8

I've noticed in different papers that after a certain number of epochs there sometimes is a sudden drop in error rate when training a CNN. This example is taken from the "Densely Connected Convolutional Networks" paper, but there are many others. I wonder what is the cause of this? Especially why it appears at the same epoch although the two architectures compared here a completely different.

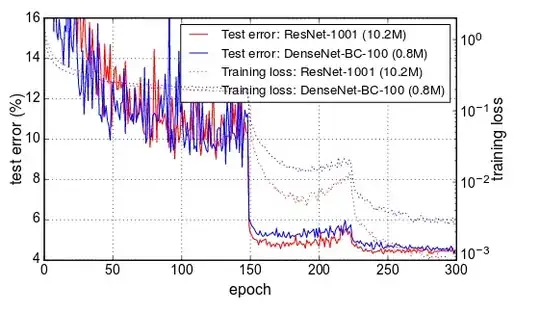
image

A similar question was asked here, but the only answer given there so far stated that it's because a saddle point in the error surface is reached and then overcome. As the two architectures are very different, they also will have a very different error surfaces (even with different dimensions), so I find highly unlikely that they both reach and overcome a saddle point at exactly the same epoch.

amoeba
  • 93,463
  • 28
  • 275
  • 317
peter griffin
  • 81
  • 1
  • 2
  • Could you perhaps share links to at least two specific papers? I wasn't aware of this – bibliolytic Nov 09 '17 at 06:29
  • for example the ResNet paper: https://arxiv.org/pdf/1512.03385.pdf and the one mentioned in the question: https://arxiv.org/pdf/1608.06993.pdf sadly in neither of them this sudden drop is explained or even pointed out – peter griffin Nov 09 '17 at 07:13
  • 1
    Most probably because of lowering the learning rate at 150 epoch, very deep networks are usually trained with SGD with a fixed learning rate schedule. You can, for example, see it again at 225 epoch. – Łukasz Grad Nov 09 '17 at 07:36
  • huh that's interesting -- within papers these things appear to happen at the same time, but it doesn't look to me like across papers this is happening at the same epoch (granted the first paper you link doesn't have epochs on the x-axis). Perhaps it's a function of the dataset? The first used imagenet, the second cifar – bibliolytic Nov 09 '17 at 07:47
  • 1
    Reducing the LR every $k$ epochs is a common strategy, but it's not the only one. For example, you could also reduce the LR if you detect that the loss is flat or increasing, which seems to be the logic used here (note how the loss has an upward trajectory before there's a dramatic decline again). – Sycorax Nov 19 '19 at 20:35
  • @ReinstateMonica I'd be interested to see your answer in the linked thread (this one I think could be closed as a duplicate). However, the real question here is WHY does the learning rate decrease result in a sudden drop of error... – amoeba Nov 20 '19 at 10:03
  • This is speculation, but I suspect it's because the curvature of the surface is changing as you move, so a step size that improves early in training is too large later in training. Consider the three cases outlined [here](https://stats.stackexchange.com/questions/364360/how-can-change-in-cost-function-be-positive/364366#364366), and then imagine what happens if we have a different expression for $x^{(t+1)}$ at each $t$. It's easy to choose a good step size when $x^{(t+1)}$ is fixed, but if it changes as we move, then we can move into a domain where $\eta$ is too large and we usually overshoot. – Sycorax Nov 20 '19 at 16:45
  • Saying "different expression for $x^{(t+1)}$ at each $t$" is a little loose, since the curvature actually depends on $x^{(t)}$, but I think you get the idea: we're not minimizing something nice like a quadratic, so the expression for $\nabla f(x)$ changes. @amoebasaysReinstateMonica – Sycorax Nov 20 '19 at 16:47

3 Answers3

4

The drops happen at the point where the learning rate is decreased, IF the information at

https://www.reddit.com/r/MLQuestions/comments/6i1at2/what_causes_these_sudden_drops_in_training_error/

is correct. It does make sense to me, but I did not verify it.

tyrex
  • 233
  • 2
  • 10
2

It's probably because learning rate scheduling is used to automatically reduce the learning rate when the optimizations reaches a plateau. Learning rate scheduling is a very common strategy for training neural networks.

But I can't exclude that some other effect could be at work. Sadly, complete descriptions of the exact procedures used to train and tune networks are not always reported in peer-reviewed studies, making it very challenging to understand what, precisely, accounts for different properties of the resulting model. If the paper does not describe using a learning rate schedule, you would have to e-mail the authors to know definitively what accounts for the steep drops in the learning rate.

Sycorax
  • 76,417
  • 20
  • 189
  • 313
2

I was wondering the same thing. If the issue is indeed the learning rate schedule. Then doesn't that imply that there is a huge opportunity to increase accuracy/speed up convergence by optimizing the schedule? It seems abit crazy that the loss gets lowered by a factor of 3 in 1 epoch by lowering the learning rate.

"we train models for 90 epochs with a batch size of 256. The learning rate is set to 0.1 initially, and is lowered by 10 times at epoch 30 and 60. "

Did they just randomly chose those numbers or have they brute forced it to find the best schedule?

I guess the point is to haver higher learning rate in the beginning since the weights are further from optimum and maybe there is a higher risk of local minima. Have anyone seen any papers comparing different LR schedules on imagenet using densenet or resnet?

From this paper https://arxiv.org/pdf/1706.02677.pdf, you can see the same drop and yes it is perfectly aligned with their learning rate schedule drop on epoch 30 and 60.

Looking at this article: https://www.jeremyjordan.me/nn-learning-rate/ On the loss topology images, i guess the point is that the first high learning rate finds the deepest valley but the lr is to high to go very deep in it. Then when lowering the LR you can descent deeper into that valley resulting in the drop in loss that we see. It could be interesting to test a schedule that drops the LR based on some calculation on the per epoch validation loss. E.g. if the slope of the validation is flattening out over the last x number of epochs then we can already decrease the LR instead of running with the same lr for e.g. 30 epochs more.

Niels Lindberg-Poulsen
  • 21
  • 2