My goal is to analyse vegetation cover data. The way the data collection works is that you throw a quadrat (0.5m x 0.5m) in a sample plot and estimate the percent cover of the target species. Here is an example:
df <- structure(list(site = structure(c(1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 3L, 3L, 3L,
3L, 3L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L), .Label = c("A",
"B", "C", "D", "E"), class = "factor"), cover = c(0.0013, 0,
0.0208, 0.0038, 0, 0, 0, 0.0043, 0, 0.002, 0.0068, 0.0213, 0,
0.0069, 0.0075, 0, 0, 0, 0.013, 0.0803, 0.0328, 0.1742, 0, 0,
0.0179, 0, 0.3848, 0.1875, 0, 0.2775, 0.03, 0, 0.0042, 0.0429
)), .Names = c("site", "cover"), class = "data.frame", row.names = c(NA,
-34L))
To visualize the data:
require(ggplot2)
ggplot(df, aes(site, cover)) + geom_boxplot() + labs(x = "Site", y = "Vegetation cover") +
scale_y_continuous(labels = scales::percent)
Since the data are percentages/proportions on the interval [0,1), I figured a zero inflated beta regression would be appropriate. I do this using the gamlss package in R:
require(gamlss)
m1 <- gamlss(cover ~ site, family = BEZI, data = df, trace = F)
summary(m1)
#******************************************************************
# Family: c("BEZI", "Zero Inflated Beta")
#
#Call: gamlss(formula = cover ~ site, family = BEZI, data = df, trace = F)
#
#Fitting method: RS()
#
#------------------------------------------------------------------
#Mu link function: logit
#Mu Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) -3.6698 0.4265 -8.605 3.21e-09 ***
#siteB 0.4444 0.5714 0.778 0.443510
#siteC 1.1225 0.5834 1.924 0.064948 .
#siteD 2.2081 0.4984 4.430 0.000141 ***
#siteE 0.3819 0.7289 0.524 0.604566
#------------------------------------------------------------------
#Sigma link function: log
#Sigma Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 2.8155 0.3639 7.738 2.54e-08 ***
#------------------------------------------------------------------
#Nu link function: logit
#Nu Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) -0.3567 0.3485 -1.024 0.315
#
#------------------------------------------------------------------
#No. of observations in the fit: 34
#Degrees of Freedom for the fit: 7
# Residual Deg. of Freedom: 27
# at cycle: 12
#
#Global Deviance: -43.22582
# AIC: -29.22582
# SBC: -18.54129
#******************************************************************
So far so good. Now on to the estimates and their standard errors:
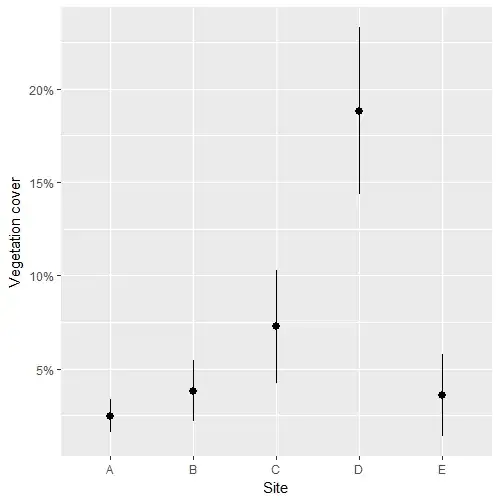
means_m1 <- lpred(m1, type='response', what='mu', se.fit=T)
df_fit <- data.frame(SITE = df$site, M = means_m1$fit, SE = means_m1$se.fit)
ggplot(df_fit, aes(SITE, M)) + geom_pointrange(aes(ymin=M-SE, ymax=M+SE)) +
labs(x="Site",y="Vegetation cover") + scale_y_continuous(labels=scales::percent)
My last point, and that's where I get stuck, is to figure out whether there are significant differences among those estimates.
My questions are (1) does this gamlss approach seems sound? and (2) is there a way to do mean comparisons for those models (i.e. posthoc tests). Or is this simply not possible with gamlss models?