How to calculate the correlation between smoking patients and heart attacks for each country?

Question

I have a set of data on smoking patients and heart attack on different time points for 25 countries.

How can I calculate the correlation between the smoking patients and heart attacks for each country?

My data look like this table1:

         Smoking             Heart Attack
Country  1988  1984  2010    1988  1984  2010
-------  ----  ----  ----    ----  ----  ----
Congo    1200  1146   675     900   400   550
Nigeria  1100   786   765     950   568   590
Zimbabwe 1098   897   900    1098   769   865
...

I am looking for a solution in R.

Answer 1

It is best to get the data into a normalized form where smoking and heart attack are separate, parallel columns and other columns provide the identifying (key) fields:

    country  year   smoking heart
1   Congo    1988      1200   900
2   Congo    1984      1146   400
3   Congo    2010       675   550
4   Nigeria  1988      1100   950
5   Nigeria  1984       786   568
6   Nigeria  2010       765   590
7   Zimbabwe 1988      1098  1098
8   Zimbabwe 1984       897   769
9   Zimbabwe 2010       900   865

In R they ought to be in a data frame:

data <- data.frame(country=c(rep("Congo", 3), rep("Nigeria", 3), rep("Zimbabwe", 3)),
                   year=rep(c(1988, 1984, 2010), 3),
                   smoking=c(1200, 1146, 675, 1100, 786, 765, 1098, 897, 900),
                   heart=c(900,400, 550, 950, 568, 590, 1098, 769, 865))

With this format, the solution is a one-liner:

by(data, data$country, function(x) cor(x$smoking, x$heart))

The output gives correlations of 0.315, 0.994, and 0.962 for Congo, Nigeria, and Zimbabwe, respectively.

However, correlations by themselves can be misleading. It is far better to look at the data:

plot(data$smoking, data$heart, col=data$country, pch=19,
 main="Heart attack and smoking, 1984-2010", xlab="Smoking", ylab="Heart attacks")
points(data$smoking, data$heart, cex=1.25)
legend(675, 1075,  levels(data$country), pch=19, col=1:length(levels(data$country)))

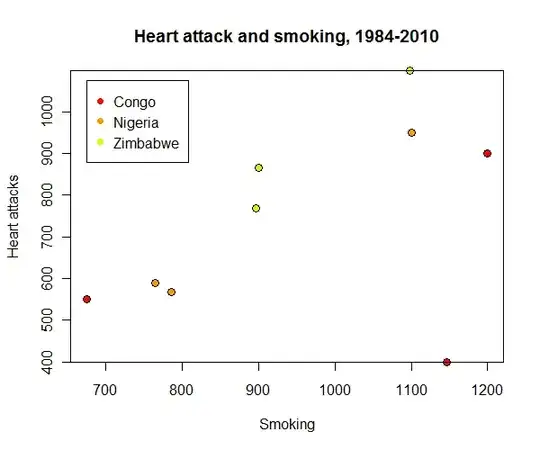
An outlying value for Congo visible in the lower right at (1146, 400) is responsible for its low correlation coefficient: the correlation is a poor description of the smoking-heart attack relation for this country's data.

Answer 2

The correlation coefficient between two variables X and Y is just Cov(X,Y)/[√Var(X)√Var(Y)] and

Cov(X,Y) = E[(X-m$_1$)(Y-m$_2$)] where m$_1$ and m$_2$ are the respective means for X and Y. Given paired observations (X$_i$,Y$_i$) for i=1,2,..,n

Cov(X,Y) is estimated by

∑ (X$_i$-m$_1$$_b$) (Yi-m$_2$$_b$)/n where m$_1$$_b$ = ∑X$_i$/n and m$_2$$_b$=∑Y$_i$/n.

The estimate for Var(X) is usually ∑ (X$_i$-m$_1$$_b$)$^2$/(n-1) and the estimate of

Var(Y) = ∑ (Y$_i$-m$_2$$_b$)$^2$/(n-1).

This tells you how to calculate the correlation coefficient. So you could write your own R code to do this. But first you need to know which Y goes with X. So you need to have the data paired. It seems that you logically would pair based on taking them from the same year. So for example the correlation coefficient for the Congo would be the estimated covariance:

{(1200-1007)(900-616.7) + (1146-1007)(400-616.7) + (675-1007) (550-616.7)}/3 divided by

[√{((1200-1007)$^2$ + (1146-1007)$^2$ +(675-1007)$^2$)/2} √{(900-616.7)$^2$ + (400-616.7)$^2$ +(550-616.7)$^2$}/2

The numbers 1007 and 616.7 appear in the formula because they represent m$_1$$_b$ and m$_2$$_b$ respectively.

Given Bill Huber's display of the data it is clear that the Congo does not follow the regression line that seems to fit well to the other countries because of one outlier in 1984. It is so extreme that it is an obvious problem based on the scatter plot. This may mean that there must be some strange reason why the high smoking rate in the Congo in 1984 does not lead to a high incidence of heart attacks in 1984 or that there is a recording error. Both possibilities should be looked into.

Looking at the other two points we see a low rate of heart attacks in 2010 and a corresponding reduction in smoking over the high rates in the 1980s and a high rate of heart attacks in 1988 associated with a high rate of smoking. This leads me to conjecture that either (1) heart attack awarness was not great in 1984 and so cases went unreported and that increased awareness between 1984 and 1988 led to better reporting and a higher rate. It seems this awareness may have led to decline in smoking in the Congo by 2010, or (2) a correct and consistent number of heart attacks occurred in 1984 but there was a data entry error on that number or (3) the much less plausible explanation that the low heart attack rate was correct but the high smoking rate was a recording error in 1984. I think (3) is doubtful because the smoking rate in 1988 is close to the recorded value for 1984 and it seems less credible that smoking rates would go up dramatically between 1984 and 1988. Nevertheless these three scenarios could explain the problem and there may be other plausible explanations that ideally should be investigated.

It is important to recognize that the 1984 outlier should not be ignored. Points like this tend to dramatically effect the correlation estimate (lowering it) as well as the variances (increasing them in this cas). In this case the outlier is noticeable without looking at multivariate outlier detection methods.

In my 1982 paper which came out of this ORNL technical report here which I have referenced on stackexchange Here shows how to calculate the influence function for the sample correlation at points in the (x,y) plane. In less obvious cases this could be helpful in identifying such outliers.