0

Using R, I have built a linear model from the fluorescence produced by a set of genetic sequences under certain experimental conditions.

The final linear model provides a number of different metrics about the model, such as RMSE, R-Squared, the estimates of the predictors' coefficients, standard errors, t-statistics, and p-values. What I would like to do is take the predictors' coefficients and standard errors and use them to predict the fluorescence of a new set of sequences whose actual fluorescence values have yet to be experimentally determined.

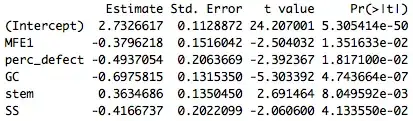
I know that one can acquire the model's coefficients and standard errors by running the command summary(model)$coefficients to get an output similar to: enter image description here

However, I am particularly confused as to how I can get a standard error of the whole model that I can use to make the confidence interval of the predicted outcome. I know that one can use confint(model, level=0.95) in order to get the upper and lower limits of the predictors, but I don't know whether it is accurate to take these numbers and use them to determine the confidence interval of the predicted outcome.

To illustrate, I would calculate the final outcome by taking the in silica calculations of new sequences and plugging them into the final model:

predicted_outcome= -0.3807*MFE1 + -0.4937*perc_defect + -0.6976*GC + 0.3635*stem + -0.4167*SS + 2.733

Then, I thought that in order to calculate the upper and lower limits of the confidence intervals, I would use values calculated by confint(model, level=0.95) to determine the predicted outcome's confidence interval.

predicted_lower_limit= -0.6768*MFE1 + -0.89817*perc_defect + -0.9553*GC + 0.0987*stem + -0.8129*SS + 2.511

predicted_upper_limit= -0.0825*MFE1 + -0.0892*perc_defect + -0.4398*GC + 0.6282*stem + -0.0203*SS + 2.954

Because I am working between building the model in R and implementing on a data frame in Python, I want to be able to calculate the predicted values and their corresponding confidence intervals on my own. Furthermore, I am not sure as to whether this approach is the proper way of understanding the confidence interval of a predicted outcome using a model. Can anybody confirm or correct this approach?

Bob McBobson
  • 103
  • 1
  • 7
  • use the predict() function this will give you predicted Y values and their standard errors based on the model and values of x that you input into the function – Michael Webb Sep 20 '17 at 17:06
  • 1
    @Great38 My apologies, I did not phrase my question properly or narrow its focus. I should have mentioned that I want to be able to calculate the upper and lower limits of the confidence interval on my own in order make the calculations in Python. Please see my edits above for further detail. – Bob McBobson Sep 20 '17 at 22:28
  • You cannot estimate the confidence interval of predictions from standard errors or confidence limits of the coefficients only. Coefficients are generally not uncorrelated. Read a textbook about regression or study the code of `predict.lm`. Or even search this site. – Roland Sep 21 '17 at 06:36
  • @Roland Alright, but given the fact that I must store this model made in R and then apply it to new data sets in the future using Python, how would recommend that I go about determining the confidence interval? I can get the predicted values themselves by plugging them into the estimated coefficients of the model, but I can't really use `predict.lm` in Python. – Bob McBobson Sep 21 '17 at 11:17
  • You should read this: https://stats.stackexchange.com/a/85565/11849 You only have to extract the necessary elements from the `lm` object and pass them to python and implement the formula for the CI in python. (I don't understand why you don't do the regression in python.) – Roland Sep 21 '17 at 11:26
  • @Roland I am using some specific model building functions in R with the caret package that I do not know how to replicate in Python. So, once the model is built in R, I exported its details as .csv file, and then my Python script later reads that .csv file in order to parse the necessary information to calculate the predictive scores. – Bob McBobson Sep 21 '17 at 11:51
  • 1
    XtX – Alexey Burnakov Sep 21 '17 at 15:57
  • this is addressed here: https://stats.stackexchange.com/a/397504/144543 – ouranos Mar 14 '19 at 14:17

0 Answers0