Does anyone tell me how to find the variance of sample median when random samples are normally distributed?? I know that I need to use the order statistics, but actually I don't understand how to apply it.
- 63,378
- 26
- 142
- 467
- 19
- 1
- 2
-
21. Is this for coursework? Can you give more context about how the issue arises? 2. What have you learned about order statistics? See [ask], in relation to search and research, and see [help/on-topic] in relation to homework-style questions. 3. Are you just after a formula? – Glen_b Sep 16 '17 at 08:18
-
https://stats.stackexchange.com/questions/41557/variance-of-sample-median and search this site for "median varianve" (a lot of posts) See also https://www.jstor.org/stable/2286545?seq=1#page_scan_tab_contents – kjetil b halvorsen Sep 16 '17 at 14:42
-
Related question seeking moments of sample median with Normal parent: https://stats.stackexchange.com/questions/303160/ – wolfies Sep 16 '17 at 16:25
-
Can you please qualify the question: standard Normal or general $N(\mu, \sigma^2)$ parent? – wolfies Sep 16 '17 at 16:27
-
Glen_b : Yes. It is about the asymptotic relative efficiency. The question compare the variance of sample mean and sample median, and these samples are normally distributed. I can derive the variance of sample mean easily, but it is hard to derive the variance of sample median, and my lecture note does not clarify how to derive it. – Si Hyun Kim Sep 17 '17 at 03:26
-
wolfies: sorry, it is the general case. – Si Hyun Kim Sep 17 '17 at 03:27
-
You can find thorough explanations from various viewpoints at https://stats.stackexchange.com/questions/45124. – whuber Sep 17 '17 at 15:39
1 Answers
I will make some illustrations with R. First, using results discussed at Central limit theorem for sample medians the asymptotic distribution of sample median of $N$ iid observations from a normal distribution is itself a normal distribution centered at the theoretical median $\mu$ and with variance $\frac{2\pi \sigma^2}{4 N}$ where $\sigma^2$ is the variance of the parent distribution. The sample median is the central order statistic, and in the case $N=2s+1$ is odd, it is the order statistic of order $s+1$, which have a distribution we can calculate exactly rather easily (theory given in the cited post and elsewhere at this site). I will use some R function I detail at the end of this post to compare the exact and approximate distributions of the sample median. We use the standard normal for parent distribution.
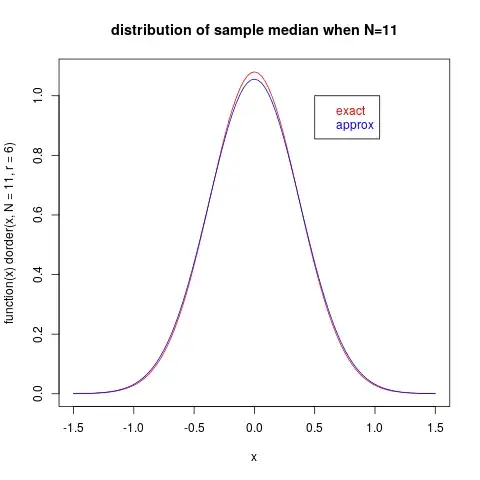
First with sample size $N=11$:
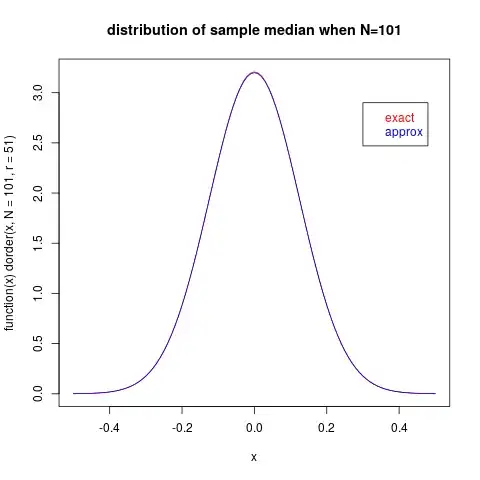
The approximation is already quite good! Let us look at the case $N=101$:
Here the approximation is virtually exact. Some R functions for distributions of order statistics:
porder <- function(x, N=1, r=1, basename="norm", ..., log.p=FALSE) {
pfun <- get(paste("p", basename, sep=""))
stopifnot(r <= N)
prob <- pfun(x, ...)
retval <- pbeta(prob, r, N-r+1, log.p=log.p)
retval
}
dorder <- function(x, N=1, r=1, basename="norm", ..., log=FALSE) {
pfun <- get(paste("p", basename, sep=""))
dfun <- get(paste("d", basename, sep=""))
stopifnot(r <= N)
logdens <- -lbeta(r, N-r+1)+(r-1)*pfun(x, ..., log.p=TRUE) +(N-r)*pfun(x, ..., lower.tail=FALSE, log.p=TRUE) + dfun(x, ..., log=TRUE)
retval <- if (log) logdens else exp(logdens)
retval
}
qorder <- function(p, N=1, r=1, basename="norm", ..., log.p=FALSE) {
pfun <- get(paste("p", basename, sep=""))
qfun <- get(paste("q", basename, sep=""))
stopifnot( r <= N)
retval <- qfun(qbeta( p, r, N-r+1, log.p=log.p), ..., log.p=FALSE)
retval
}
rorder <- function(n, N=1, r=1, basename="norm", ...) {
qfun <- get(paste("q", basename, sep=""))
qfun( rbeta(n, r, N-r+1), ... )
}
- 63,378
- 26
- 142
- 467