Uncertainty in Binary Classification of New Data (via Random Forest)

Question

We trained a binary classification RF and validated it with a test set of about N=300 entries. Here are the performance statistics:

We now would like to classify a production set of a couple of million items. If we just do that, the output of that will be p TRUE and 1-p FALSE where p lies within [0,1].

However, because we have a certain FP- and FN-Rate, this result/ratio comes with some uncertainty, right?

For that reason, we would like to quantify this uncertainty, e.g. with a 95% confidence interval, based on our performance measures. E.g. something like: With 95% probability, 20-25% of items in the production set are TRUE, 75-80% are FALSE. These numbers probably don't even add up, the range for TRUE would be sufficient.

Also, all these performance measures displayed above come with their own confidence intervals, maybe these could be considered too in that uncertainty calculation?

Bonus-Question: We used the caret package in R. Is there some sort of a function (in caret or in another R package) to do this automatically?

Answer 1

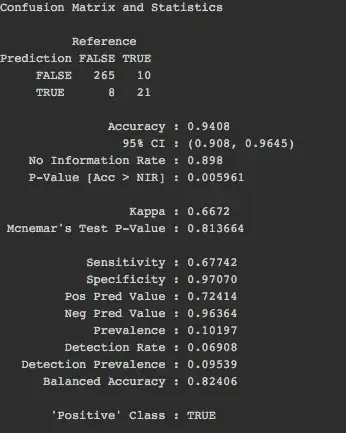
I get to your main question in the second paragraph, first a more general remark: You probably already know that you should not be optimizing accuracy with a data-set that has this level of class imbalance because there is probably also classification cost imbalance. (You imply that there is when you say you are mainly interested in the true class. If there isn't, then the problem is trivial and you can in your case have almost 90% accuracy without even constructing a classifier.) Most likely, a true record predicted as false is a bigger problem than the other way around. It is more important to identify the few true records and it can be tolerated to identify some more false records as true to get there. As you said, tree based algorithms provide per predicted record a probability that it belongs to the class true which you call $p$. You are not forced to put the cutoff at $p=0.5$, you can put it lower to make sure you don't miss the few true records. The relative misclassification costs between false positives and false negatives, as determined by your application scenario, can tell you where to put the cutoff.

To understand what this number $p$ means and what can be done with it, we need to look at the tree classifier. All your training set records have started at the tree's root, branched multiple times according to rules that the algorithm finds in the data and end up in a leaf. The goal is to have relatively pure leaves, each leaf being dominated by records of one class. (You could have perfectly pure leaves if you just keep branching, but you would be overfitting on your training set.) $p$ is the proportion of records in that leaf that are of the class you are trying to identify. This number loosely follows a frequentist interpretation of probabilities: If the record is part of this leaf, it has x out of y chances of being that class.

A forest is just a collection of trees that have been randomized (the variables to branch on are chosen randomly rather than to optimize gains in purity) and left unpruned (you branch till all leaves are pure). Each record is rooted through all the trees in the forest. $p$ is computed slightly differently here: It denotes the proportion of trees in the forest where this record ends up in a leaf dominated by this class. The probability within each tree would be binary since the leaves are pure in the absence of pruning. It only makes sense to compute $p$ on forest level.

Knowing how those values of $p$ are derived, I don't see how it would be possible to construct confidence intervals around every single one of them. Even if it was possible, it wouldn't be very practical, you would have one CI per record in your production set.

I also don't think you can or should make the kind of pronouncements you want to make on a data-set level ("With 95% probability, 20-25% of items in the production set are TRUE, 75-80% are FALSE"). Because of your class imbalance, you don't want to find out how many records exactly are true (according to a 0.5 cutoff), you want to bias that number upwards (by lowering the cutoff) so that you don't miss the true records. What you should do is determine your misclassification costs, put them in a loss function and then optimize that.

Also, once that you have chosen your model based on test set performance, you can retrain that same model (same number of trees in the forest same type of randomization etc.) with all the labeled data you have available. It was good to set a test set aside in order to choose a model. Once that is done, you want to use all the information you have to train a model which you will use for your unlabeled production set.

Answer 2

If I understand your question correctly, I think it has been answered before:

Confidence Interval - Binary classification

Also be careful when interpreting confidence intervals:

From OpenIntro

A careful eye might have observed the somewhat awkward language used to describe confidence intervals. Correct interpretation:

We are [XX]% confident that the population parameter is between...

Incorrect language might try to describe the confidence interval as capturing the population parameter with a certain probability. This is one of the most common errors: while it might be useful to think of it as a probability, the confidence level only quantifies how plausible it is that the parameter is in the interval.
As we saw in Figure 5.2, the 95% confidence interval method has a 95% probability of producing an interval that will contain the population parameter. A correct interpretation of the confidence level is that such intervals will contain the population parameter that percent of the time. However, each individual interval either does or does not contain the population parameter. A correct interpretation of an individual confidence interval cannot involve the vocabulary of probability.
Another especially important consideration of confidence intervals is that they only try to capture the population parameter. Our intervals say nothing about the confidence of capturing individual observations, a proportion of the observations, or about capturing point estimates. Confidence intervals only attempt to capture population parameters.