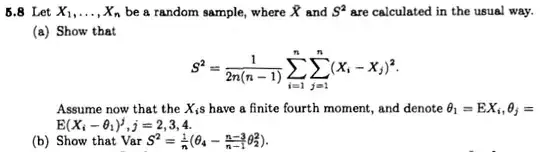12

In his answer to my previous question, @Erik P. gives the expression $$ \mathrm{Var}[s^2]=\sigma^4 \left(\frac{2}{n-1} + \frac{\kappa}{n}\right) \>, $$ where $\kappa$ is the excess kurtosis of the distribution. A reference to the Wikipedia entry on the distribution of the sample variance is given, but the wikipedia page says "citation needed".

My primary question is, is there a reference for this formula? Is it 'trivial' to derive, and if so, can it be found in a textbook? (@Erik P. couldn't find it in Mathematical statistics and data analysis nor I in Statistical Inference by Casella and Berger. Even though the topic is covered.

It would be nice to have a textbook reference, but even more useful to have a (the) primary reference.

(A related question is: What is the distribution of the variance of a sample from an unknown distribution?)

Update: @cardinal pointed out another equation on math.SE: $$ \mathrm{Var}(S^2)={\mu_4\over n}-{\sigma^4\,(n-3)\over n\,(n-1)} $$ where $\mu_4$ is the fourth central moment.

Is there some way that to rearranged the equations and resolve the two, or is the equation in the title wrong?

Community
  • 1
Abe
  • 3,561
  • 7
  • 27
  • 45
  • 1
    I don't think that formula is correct. – cardinal Jun 06 '12 at 15:45
  • Related: http://math.stackexchange.com/a/73080/7003 – cardinal Jun 06 '12 at 15:46
  • that related question was asked by @byron-schmuland – Abe Jun 06 '12 at 16:57
  • 2
    I think you mean *answered*, not *asked*. The formula given in this question is incorrect; as Byron's answer nicely demonstrates. :) – cardinal Jun 06 '12 at 16:58
  • Unfortunately, such pinging doesn't work unless he's already participated in the comment stream. :( (It appears he has taken notice following the comment you posted on the question on the math site.) Cheers. – cardinal Jun 06 '12 at 17:09

2 Answers2

16

Source: Introduction to the Theory of Statistics, Mood, Graybill, Boes, 3rd Edition, 1974, p. 229.

Derivation: Note that in the OP's Wikipedia link, $\kappa$ is not the kurtosis but the excess kurtosis, which is the "regular" kurtosis - 3. To get back to the "regular" kurtosis we have to add 3 in the appropriate place in the Wikipedia formula.

We have, from MGB:

$\text{Var}[S^2] = {1\over{n}}(\mu_4 - {{n-3}\over{n-1}}\sigma^4)$

which, using the identity $\mu_4 = (\kappa + 3)\sigma^4$, can be arranged to (derivation mine, so any errors are too):

$ = {1\over{n}}(\kappa \sigma^4 + {{n-1}\over{n-1}}3\sigma^4 -{{n-3}\over{n-1}}\sigma^4) = \sigma^4\left({\kappa \over{n}}+{3(n-1)-(n-3)\over{n(n-1)}}\right) = \sigma^4\left({\kappa\over{n}} + {{2}\over{n-1}}\right) $

jbowman
  • 31,550
  • 8
  • 54
  • 107
  • 2
    (+1) Nearly 40 years since the last edition, MGB is still the best beginning/intermediate introduction to math stat. It's a shame it has been out of print in the Western world for so long. – cardinal Jun 06 '12 at 21:02
  • I found a [pdf of MGD](http://www.colorado.edu/Economics/morey/7818/MoodGraybillBoesBook/MGB3rdSearchable.pdf), but there is no citation to the original proof. Which is okay, but it would be nice to know where to find it. – Abe Jun 06 '12 at 22:50
  • The actual derivation of the result is not in MGB, but rather us relegated to problem 5(b) on page 266. – cardinal Jun 06 '12 at 22:54
  • Yes, not all statements come with proofs, but at least this one is in the text, not relegated to a question, and there's an outline of the approach to the proof on p. 230. – jbowman Jun 06 '12 at 22:56
  • 1
    @Abe: You will almost certainly not find an "original" reference for this. It is not the sort of standalone "publishable" result found in academic journals. It is simply a (rather tedious) calculation following from the basic properties of mathematical expectation. Quoting a textbook like MGB is perfectly reasonable and acceptable. – cardinal Jun 06 '12 at 22:57
9

It is not clear if this will suit your needs for a definitive reference, but this question comes up in the exercises of Casella and Berger:

(page 364, exercise 7.45 b):

enter image description here

With reference to exercise 5b that provides another variant, in which $\Theta_2$ and $\Theta_4$ are the second and fourth moments ($\sigma^2$ and $\kappa$), respectively:

enter image description here

These are equivalent to the equation given in an answer on math.SE:

$\mbox{Var}(S^2)={\mu_4\over n}-{\sigma^4\,(n-3)\over n\,(n-1)}$

Community
  • 1
David LeBauer
  • 7,060
  • 6
  • 44
  • 89
  • It is interesting that your link and my link (in the comments to the OP) are different, but point to the same place. – cardinal Jun 06 '12 at 16:30
  • 2
    @cardinal - I just copy-pasted from the OP - but the last digits are the user id of the person who copies the link, e.g. my link would be http://math.stackexchange.com/a/73080/3733 – David LeBauer Jun 06 '12 at 16:33
  • Aha! (+1) I did not notice that the last part of the link was one's own id! Thanks for pointing that out. We're being followed... – cardinal Jun 06 '12 at 16:39
  • it is good to have a trustworthy reference, but would still be nice to track down the original. +1 for looking through the exercises. – Abe Jun 06 '12 at 16:39
  • @cardinal one justification for / use of tracking is the badges for sharing links (announcer, booster, publicist) – David LeBauer Jun 06 '12 at 16:44
  • Good point. Poor attempt at humor on my part, though. :) – cardinal Jun 06 '12 at 16:45
  • @cardinal I did not realize any of this until you brought it up ... your point is well taken. – David LeBauer Jun 06 '12 at 16:51
  • not only would it be nice to track down an original reference, but I think it would be necessary to have one (that is not to an exercise) for a publication. – Abe Jun 06 '12 at 16:54
  • @Abe: If you're looking for an authoritative reference, you might look in the classical Johnson & Kotz volumes. It's bound to be in one of them; they're pretty exhaustive. The computation, while tedious, is routine, though. – cardinal Jun 06 '12 at 16:56
  • I did a simulation, it seems formula 5.8a is wrong... – hihell Nov 18 '20 at 18:30
  • @hihell can you share your code? – David LeBauer Dec 03 '20 at 18:48
  • @DavidLeBauer as you can see in pairwise2, 2n*(n-1) is wrong https://gist.github.com/hihell/a578251c0497d3a8abe82db4e4088093 – hihell Dec 07 '20 at 18:44