3

Question

Is it correct to test the difference of a measurement between groups using generalized least squares?

Example

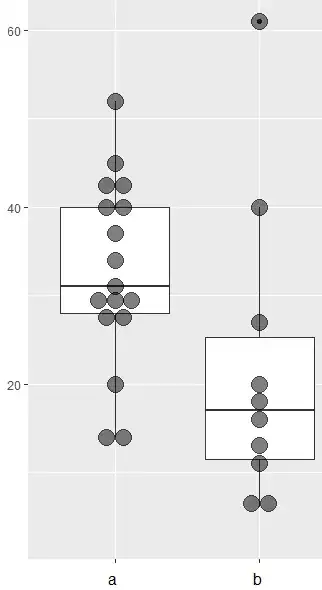
My data looks like this:

enter image description here

I perform a gls in R, but I`m not sure if it is a correct method. Usually I dont have categorical variables and I just applied these functions because I always do.

lsmeans(gls(outcome ~ group, data = mydata, pairwise ~ group, adjust="tukey")

$lsmeans
 group   lsmean       SE df lower.CL upper.CL
 a     32.64706 3.219347 25 26.01669 39.27743
 b     21.90000 4.197515 25 13.25506 30.54494

Confidence level used: 0.95 

$contrasts
 contrast estimate       SE df t.ratio p.value
 a - b    10.74706 5.289927 25   2.032  0.0530

Here group is a factor and outcome is numeric. If this is a correct approach, what would this test be called?

Alternative

If I perform a t test, which might be more correct after thinking about it, the P value is doubled compared to the method above. Is that due to the method, or due to the fact that one reports "a minus b" and the other "a compared to b" ?

t.test(outcome ~ group, mydata)

    Welch Two Sample t-test

data:  outcome by group
t = 1.8015, df = 13.182, p-value = 0.09454
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -2.123109 23.617227
sample estimates:
mean in group a mean in group b 
       32.64706        21.90000
Leo
  • 465
  • 1
  • 5
  • 18
  • 1
    (1) Why would you want to use GLS for this in the first place? (2) Are you aware that by default, R's `t.test` uses Welch's $t$-test, which is not the same as the traditional kind with an assumption of equal variances? If you want the equal-variances assumption, give `t.test` the argument `var.eq = T`. – Kodiologist Aug 11 '17 at 17:28
  • @Kodiologist Well I just altered my standard code that I use when I have continuous dependent variables, I also suspected a t test would be more appropriate. I then immediately performed a t test and saw that the p value was very different, hence my question.No I was not aware of that assumption, thanks will change that immediately. Do you think a GLS is not appropriate? That would answer my question. – Leo Aug 11 '17 at 17:30
  • 1
    I'm not familiar enough with GLS to say whether the model is correct, but certainly it seems like overkill if all you want is to test whether the means of two independent samples are equal. – Kodiologist Aug 11 '17 at 17:45
  • 2
    Your `gls` model is equivalent to an `lm` model. Why don't you use `lm`? – Roland Aug 14 '17 at 06:18
  • @Roland Well I just used the code I normally use, but you're right `glm` is even more overkill than `lm`. But even `lm` is perhaps also overkill and probably not a correct approach I`m thinking. Probably just need to do a t test. Do you agree? – Leo Aug 14 '17 at 08:34
  • 1
    If you want to test the difference in means between two samples and are confident that the test's assumptions are fulfilled, you can obviously use a t-test. Why are you even asking? – Roland Aug 14 '17 at 08:41
  • @Roland My question was whether using a linear model is a correct approach. I just used my standard code as a first try, before thinking about how to do it. Then I thought about how to do it and did a t test and saw the results were different (but as Kodiologist points out, I have an error in the way I called the t-test). That is why I asked if my first approach would also be correct. I also say that in the question. – Leo Aug 14 '17 at 08:49
  • 1
    See: https://stats.stackexchange.com/a/76292/149550 – klumbard Aug 14 '17 at 12:43

1 Answers1

1

As pointed out in the comments by Kodiologist and Roland, using a linear model seems overkill, but is not necessarily incorrect. Kodiologist pointed out that the t.test() call was incorrect, as it assumes unequal variance by default.

Calling the t.test with explicitly stating every argument gives exactly the same difference and significance as glm does. And as Roland points out, as lm would.

t.test(outcome ~ group, 
    mydata, 
    alternative = c("two.sided"), 
    paired=FALSE, 
    var.equal=TRUE, 
    conf.level=0.95)

Perhaps the two approaches are equivalent since the results are exactly the same and using a linear model does not seem incorrect, just overly complicated. I`m still unsure what testing this with a linear model would be called.

Leo
  • 465
  • 1
  • 5
  • 18
  • 2
    If you look at the summary output of the linear model you see a t-value. The null hypothesis tested is that the coefficient equals zero. Since (when using the default treatment contrasts) the coefficient is an estimate of the difference between group means, the linear model is mathematically equivalent to the t-test. In fact, R uses `lm` as the basis of its `aov` function and a t-test is equivalent to an ANOVA if you have only two groups. – Roland Aug 14 '17 at 11:45
  • That makes it much more understandable, thanks. If you want you could put it in an answer, you explain it better. – Leo Aug 14 '17 at 11:51