2

For example, if I generate density with R code

D = c(rnorm(100,1,1), rnorm(100,5,1))

Then the following density will follow:

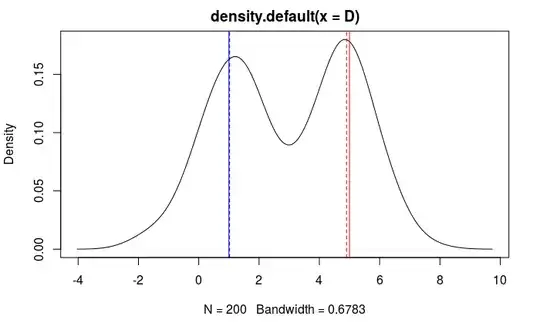
enter image description here

We can find the primary peak location by 

density(D)$x[which(density(D)$y == max(density(D)$y))]

But how to find the secondary peak?

John
  • 263
  • 2
  • 12
  • You can find the n'th largest number in R by: sort(x, TRUE)[n] - where x is vector of numbers. – Repmat Aug 10 '17 at 06:38
  • 2
    @Repmat but the second largest number in density values might not be the value of the second peak. It could be a point next to the first peak which is still larger than the second peak. – John Aug 10 '17 at 06:43
  • 1
    You're looking for local maxima. The answer to [this question](https://stats.stackexchange.com/questions/30750/finding-local-extrema-of-a-density-function-using-splines) could help. – Alex Firsov Aug 10 '17 at 06:43
  • 2
    Alternatively, you could write a function with some optimization technique (think Newton's method etc) to identify the maxima in `density(D)$y` and then store them away. Then sort the vector, and voila! – Alex Firsov Aug 10 '17 at 06:46

2 Answers2

5

You can use mixture models to capture the biomodality

library(flexmix)
set.seed(42)

D <- c(rnorm(100,1,1), rnorm(100,5,1))
kde <- density(D)
m1 <- FLXMRglm(family = "gaussian")
m2 <- FLXMRglm(family = "gaussian")
fit <- flexmix(D ~ 1, data = as.data.frame(D), k = 2, model = list(m1, m2))
c1 <- parameters(fit, component=1)[[1]]
c2 <- parameters(fit, component=2)[[1]]




> c1
                  Comp.1
coef.(Intercept) 1.022880
sigma            1.031319


> c2
                  Comp.2
coef.(Intercept) 4.9042434
sigma            0.9081448

plot(kde)
abline(v=1, col='blue')
abline(v=c1[[1]], lty=2, col='blue')
abline(v=5, col='red')
abline(v=c2[[1]], lty=2, col='red')

enter image description here

rightskewed
  • 3,040
  • 1
  • 14
  • 30
2

If you can assume that you have a mixture of normal distributions, simply use a mixture model:

set.seed(42)
D = c(rnorm(100,1,1), rnorm(100,5,1))

library(mixtools)
mD <- normalmixEM(D)
mD$mu
#[1] 1.079553 4.918794
summary(mD)

plot(mD, which=2)
lines(density(D, "SJ"), lwd = 2)

resulting plot

If you really need the exact peak locations of the combined density function, you have all necessary values available (mixing proportion, means and standard deviations) for calculating the maxima. I don't have time to figure out the maths right now, but it shouldn't be too hard.

Roland
  • 5,758
  • 1
  • 28
  • 60