4

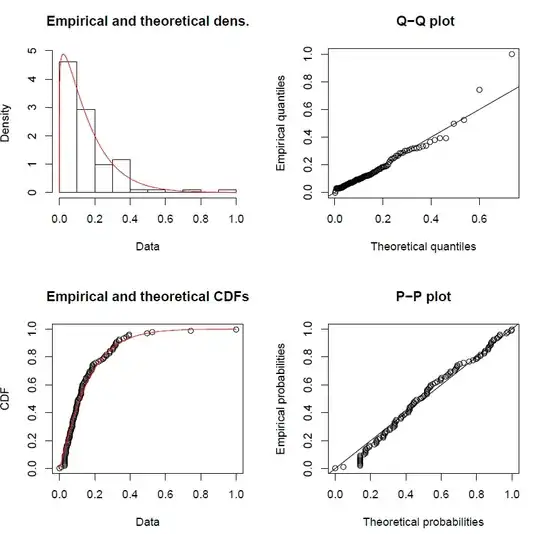
I tried to fit my data to the Weibull and I got the following output:

enter image description here

I then used R to generate 10,000 bootstrapped parameters of fit values for a and I got this output (image2):

Does this mean the distribution of my data fit well with a weibull distribution of the shape and size, approximated by bootstrapping?

enter image description here

library(ggplot2)
library(ggpmisc)
library(RColorBrewer)
library(Cairo)
library(grid)
library(moments)
library(fitdistrplus)
library(logspline)
library(adSim)
library(MASS)
library(car)
library(plot3D)

df <- read.csv("c:/master.csv", header=T, sep=",")
df[!(rowSums(is.na(df))),]
attach(df)
mp <- subset(df)
#mp <- subset(df, mars == "x")
grades <- mp$SCBO
gradena <- na.omit(grades)

data <- as.numeric(gradena)

range01 <- function(x){ (x - min(x))/(max(x)-min(x)) * (0.99999999 - 
0.00000001) + 0.00000001 }
data2 <- range01(data)
ft <- fitdist(data2, "weibull")

plot(ft)
gofstat(ft)


b.ft <- bootdist(ft,niter=10001)
summary(b.ft)
plot(b.ft, col = ramp.col(col = c("darkred","blue","green"), 
n = 10001, alpha = 0.4))
Steffen Moritz
  • 1,564
  • 2
  • 15
  • 22
user170796
  • 41
  • 1
  • Please register &/or merge your accounts (you can find information on how to do this in the **My Account** section of our [help]), then you will be able to edit & comment on your own question. – Silverfish Jul 22 '17 at 20:30

2 Answers2

1

In plain English: you sampled some data from population of interest and obtained a point estimate for some parameter. If you obtained different sample, you could obtain a different estimate. The range of possible differences between such estimates, obtained on different samples from your population, can be quantified by measuring their errors. One of the ways to achieve so is to use bootstrap. Basically, bootstrap imitates the sampling process: you are sampling from your data, the same way as you would sample your cases from the population. By doing so, you learn about possible variability of your estimates. Obviously the procedure is limited by your data, so if the sample is far from representative for the population, then it can underestimate, or overestimate the error. So bootstrap is a procedure to learn about possible variability of your estimates.

Tim
  • 108,699
  • 20
  • 212
  • 390
0

Tim has given a good explanation of what bootstrapping does, and of its limits.

So to answer your question on whether the result means that it is a Weibull distribution: empirical distributions will never follow a theoretical distribution 100%. (But it does not look too far off to me.) Therefore, you will not find a perfect match. The question is, can you find another distribution which matches better?

I think you should try to fit some similar distributions and compare the outputs of the summary commands for them. Visual inspection and the loglikelihood, AIC and BIC values given in the output can tell you which one fits best.

The one that fits best will also not match 100%. But it is your best choice.

John Silver
  • 65
  • 7