1

The scatter plot shows two data series (x,y) the are placed somehow around a tilted ellipse. This is in fact the way I have drawn this example plot.

Which statistics of the data sets are the most suitable to estimate back the geometrical parameters of the underlying ellipse? The objective is to have an ellipse that deviates the least from the points (perhaps considering distances in direction normal to the ellipse?). Such parameters could be the location of the centre, the lengths of the major and minor axes and, interestingly, the tilt with respect to the x axis. 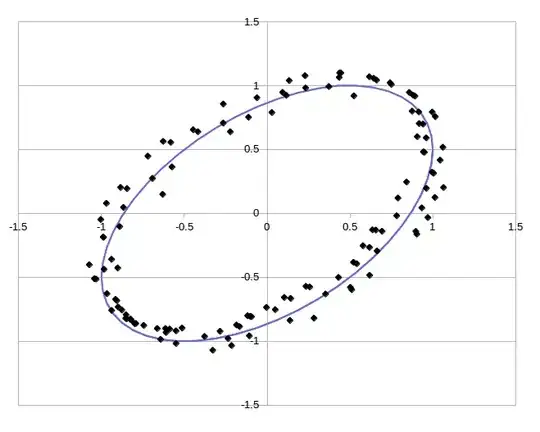a plot of an ellipse and points scattered around it There are many mathematical representations for an ellipse -- using any that is amenable to a statistical interpretation would do.

Community
  • 1
XavierStuvw
  • 115
  • 5
  • @Glen_b Yes this is a duplicate. Thanks for pointing out this alternative post. – XavierStuvw Jun 30 '17 at 10:42
  • **Note** While the question is a duplicate or near such, the answer to this post may have some merits compared with the answer in the alternative. – XavierStuvw Jun 30 '17 at 10:53

1 Answers1

2

You can use the fact that the sum of the distance to the two foci ($A$ and $B$) is constant for each point $X_i$ of the ellipse and perform a minimization of the Loss function $$L=\left( \left\lVert X_i-A\right\rVert +\left\lVert X_i-B\right\rVert-l\right)^2 $$ where the norm is the euclidian distance and the parameters are the coordinates of $A$ and $B$ and $l$ (5 parameters in total)

François Darmon
  • 581
  • 4
  • 4
  • So I need at least a mere 5 points to close the problem, and the more the merrier. This is indeed in line with the logic of https://stats.stackexchange.com/a/268986/133721 – XavierStuvw Jun 30 '17 at 10:41
  • 1
    This is mathematically clever. It would be more satisfactory from a statistical point of view if it were augmented by (a) a description of how $L$ would be minimized--it's nonlinear in all five parameters--and, more importantly, (b) an account of how the variance matrix of the parameter estimates could be computed so that the uncertainties in the solution could be evaluated. One would also be interested in the stability of the solution: what would happen to it if, say, the ellipse were sampled unevenly? I suspect it might perform very well for highly eccentric ellipses, but I'm not sure. – whuber Jun 30 '17 at 13:34