Frequency of occurrence (FO) is a simple metric measuring the proportion of samples (often expressed as a percentage) where a certain item is present. It can be calculated as follows:
$FO= 100\% \times \frac{n}{N}$, where n is the number of samples where a certain item was observed and N the total number of samples.
For binary data, FO is equivalent to average of a binary vector multiplied by 100%. I.e:
x <- c(rep(1, 5), rep(0, 5))
x
# [1] 1 1 1 1 1 0 0 0 0 0
100*mean(x)
# [1] 50
Following this logic, it is possible to calculate standard deviation for the FO estimate:
100*sd(x)
# [1] 52.70463
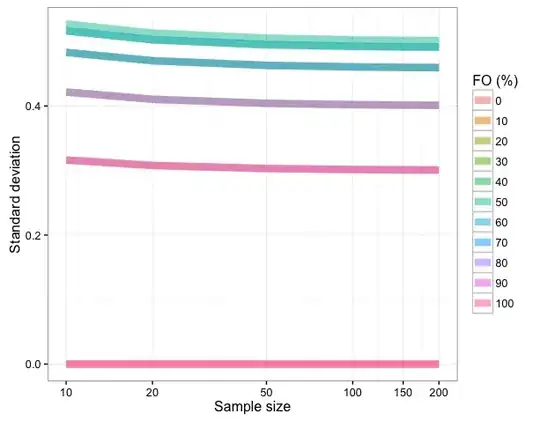
Yet the standard deviation appears to be affected by the number of observations:
100*mean(c(rep(1,5*10^6), rep(0,5*10^6)))
# [1] 50
100*sd(c(rep(1,5*10^6), rep(0,5*10^6)))
# [1] 50
But does not seem to converge the FO estimate in every case:
100*mean(c(rep(1,2*10^6), rep(0,8*10^6)))
# [1] 20
100*sd(c(rep(1,2*10^6), rep(0,8*10^6)))
# [1] 40
My questions are:
1) What does standard deviation mean in practice for frequency of occurrence?
2) Is this metric or other variance derivates (standard error, confidence intervals) useful for expressing the uncertainty of a FO estimate?