I have read and seen a lot of Parallel coordinates plots. Can someone answer the following set of questions:
It seems to me that the main function of PCP is to highlight homogeneous groups of individuals, or conversely (in the dual space, by analogy with PCA) specific patterns of association on different variables. It produces an effective graphical summary of a multivariate data set, when there are not too much variables. Variables are automatically scaled to a fixed range (typically, 0–1) which is equivalent to working with standardized variables (to prevent the influence of one variable onto the others due to scaling issue), but for very high-dimensional data set (# of variables > 10), you definitely have to look at other displays, like fluctuation plot or heatmap as used in microarray studies.
It helps answering questions like:
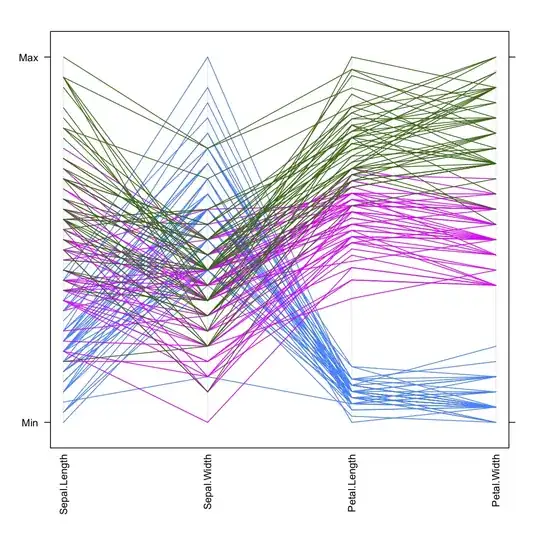
In the following plot of the Iris data, it is clearly seen that species (here shown in different colors) show very discriminant profiles when considering petal length and width, or that Iris setosa (blue) are more homogeneous with respect to their petal length (i.e. their variance is lower), for example.
You can even use it as a backend to classification or dimension reduction techniques, like PCA. Most often, when performing a PCA, in addition to reducing the features space you also want to highlight clusters of individuals (e.g. are there individuals who systematically score higher on some combination of the variables); this is usually down by applying some kind of hierarchical clustering on the factor scores and highlighting the resulting cluster membership on the factorial space (see the FactoClass R package).
It is also used in clustergrams (Visualizing non-hierarchical and hierarchical cluster analyses) which aims at examining how cluster allocation evolves when increasing the number of clusters (see also, What stop-criteria for agglomerative hierarchical clustering are used in practice?).
Such displays are also useful when linked to usual scatterplots (which by construction are restricted to 2D-relationships), this is called brushing and it is available in the GGobi data visualization system, or the Mondrian software.
In regards to questions 3, 4, and 5 I would suggest you check out this work
To sum up their findings people are ok at identifying the direction of the slope of the relationship between each node, but aren't that good at identifying the strength of the relationship or the degree of the slope. They give suggested levels of noise in which people can still decipher the relationship in the article. Unfortunately the article does not discuss identifying subgroups via color like chl demonstrates.
Please visit http://www.cs.tau.ac.il/~aiisreal/ and also look at the new book
Parallel Coordinates - This book is about visualization, systematically incorporating the fantastic human pattern recognition into the problem-solving process... www.springer.com/math/cse/book/978-0-387-21507-5.
In Ch. 10 there are lots of real examples with multivariate data showing how parallel coordinates (abbr. ||-cs) can be used. It is also worth learning some of the math to visualize and work with multivariate/multidimensional relations (surfaces) and not just point sets. It is fun seeing and working with the analogues of familiar objects in many dimensions i.e. Moebius strip, convex sets and more.
In short ||-cs are a multidimensional coordinate system where the axes are parallel to each other allowing for lots of axes to be seen. The methodology has been applied to Conflict resolution algorithms in Air Traffic Control, Computer Vision, Process Control and Decision Support.
