2

It is inherently impossible to know the probability distributions of random variables we might encounter in the "wild" -- that is the reason why researchers have to take samples.

However, since the underlying distribution is inherently a "black box", it seems like an ideal analysis would make as few assumptions about it as possible.

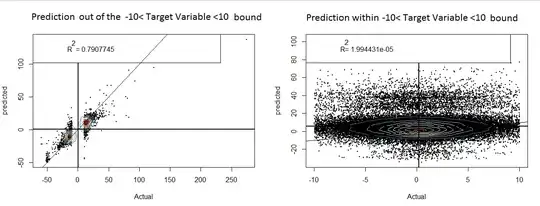
In order for the central limit theorem (CLT) to apply for i.i.d. variables following a certain distribution, it is necessary that the second moments of that distribution are finite. However, if we take a "typical" distribution, or distribution "at random", that distribution does not have finite second moments. (At least, if I interpret the comments on this question at Math.SE correctly. EDIT: this was deleted -- see below for screenshots of my stupid question and comments.)

As far as I understand, it is usually the default assumption that the CLT will hold. But combining the facts that (1) assumptions about unknown distributions should be as minimal as possible (2) the typical distribution does not satisfy the CLT, isn't this the exact opposite of what would be good?

Question: Shouldn't we assume by default, instead, that the CLT does not hold for an arbitrary unknown distribution? What is the justification for the opposite practice?

One might argue that it would be easy to identify "heavy-tailed" distributions which don't satisfy the CLT from sample data. But I don't think this is the case. Superficially, the PDF's of the normal and Cauchy distribution are both bell-shaped and look very similar. Moreover, looking at a QQ-plot for (the sample distribution of) the Cauchy distribution, it seems like a matter of luck whether we'll sample enough outliers to confirm a suspicion that the distribution is "fat-tailed", see e.g. (1)(2).

And the Cauchy distribution is just one example of a distribution which doesn't satisfy the CLT -- there are infinitely many, and in some sense "far more" such distributions than distributions which do satisfy the CLT.

I have heard that people have argued that the failure to account for fat-tailed distributions was a contributing factor to the 2008 financial crisis (1)(2), an event which obviously had a massive societal implications. Yet at least one investor website still acts as if the CLT being satisfied is a valid default assumption, despite the (1) enormously negative potential consequences for doing so, and (2) the aforementioned reasons why such a default assumption might be invalid.

enter image description here enter image description here enter image description here

Chill2Macht
  • 5,639
  • 4
  • 25
  • 51
  • 1
    The linked Q at math SE was removed. – kjetil b halvorsen May 13 '20 at 14:31
  • @kjetilbhalvorsen Good point -- I added it below the body of this question – Chill2Macht May 16 '20 at 20:16
  • " However, if we take a "typical" distribution, or distribution "at random", that distribution does not have finite second moments." - what makes you think so? – Aksakal Jun 22 '20 at 21:28
  • @Aksakal look at characteristic functions -- finite second moments correspond to twice differentiability. the vast majority of once differentiable functions are not twice differentiable, and the vast majority of continuous functions are not differentiable. I think even the vast majority of differentiable functions are not even continuously differentiable, and the vast majority of once continuously differentiable functions are not twice differentiable (continuously or otherwise). also see the deleted math.se question copy-pasted at bottom where Did explains this measure theoretically – Chill2Macht Jun 26 '20 at 03:48
  • @Chill2Macht, these are just conjectures about "vast majority," I don't see any argument about observed distributions in Nature. what you call "theoretically" is not really theoretical, because you don't provide any solid reasoning here, just statements, that are not even obvious to anybody. "vast majority" of functions are not densities, and it's hard for me to bend my mind to imagine that densities functions in nature are not twice differentiable – Aksakal Jun 26 '20 at 03:55
  • @Aksakal they are not conjectures (or "just statements" absent "solid reasoning"), take a real analysis or topology course, they are well known theorems, you can google this or look it up on Wikipedia for yourself. If you don't like the question's premise, then just downvote it and move on. (No mind bending is required, just a solid mathematics education.) See here: https://math.stackexchange.com/a/145683/327486 If you have a separate question please ask a separate question – Chill2Macht Jun 26 '20 at 03:58
  • No, I don’t downvote like that. I am suggesting you to work on your argument. It’s unconvincing and weak. Your wild references to topology do not help at all. Bring up specific theories from topology if you think they can form a good reason. Since it is you who is peeing in the wind here, the burden is on you to show that distributions in nature have no second moment. I know some that do not have second moment in physics but wouldn’t say that they are a common place – Aksakal Jun 26 '20 at 04:08

1 Answers1

2

I have written a proof that for the general case involving exponential growth, the CLT cannot hold and in most cases, no admissible non-Bayesian estimator exists. This includes stocks, cancer growth and a number of applications in physics. I have also derived the general rules for use in those cases.

The historic use of Gaussian models, in particular, came out of punch card and slide rule computing. I would not agree with you that we should assume the CLT does not hold, but rather more time should be spent investigating what does hold and why. For exponential growth, excluding some interesting special cases, all distributions are some transformation of the Cauchy distribution.

It will require some retraining because not all axiomatic systems of probability will support the mathematics required. It is one of the unusual cases where your axioms determine your outcome. Where the axioms do not support it, you can prove no solution can exist. One of the peculiar results of this is that fundamental concepts like the capital asset pricing model lead to a mathematical contradiction under certain axiom systems and can be proven to be without a solution in others. In those systems, it is a valid model that cannot be solved.

You can view the relevant papers at https://papers.ssrn.com/sol3/cf_dev/AbsByAuth.cfm?per_id=1541471

Any claim that is important has been tested empirically against the population of data available. I am hoping to add a conjecture by the end of summer that there is a branch of stochastic calculus that has not been noticed to exist by anyone. I can solve the simple cases but mathematicians and statisticians will need to go do a serious look at the boundaries.

The paper on distributions is under revisions and I hope to have a new, complete version in a week or two.

Dave Harris
  • 6,957
  • 13
  • 21
  • 1
    Can you state the specific paper names in your answer? I tried to look at the papers at the link you provided, but had difficulty connecting different parts of your answer to the different papers found on the webpage. – Chill2Macht Jun 14 '17 at 13:56
  • 2
    @Chill2Macht read "The Distribution of Returns." It covers the financial market case. – Dave Harris Jun 14 '17 at 17:03