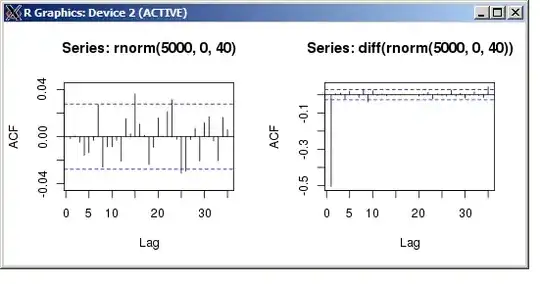
If I understand your comments correctly, you've overdifferenced, which is talked about in various guides.
EDIT:
Your original series of numbers (rnorm(5000, 0, 40)) has, by definition and design, no relationship between adjacent numbers or every 2nd number or every 3rd number. It's "random" (pseudo-random, but not distinguishable from truly random by us mere mortals). So the ACF you calculate is random garbage.
But differencing takes that series of numbers and creates a new series which is related in a particular, deterministic way: subtraction of adjacent values. Consider your initial random number series: $(n_1, n_2, n_3, ...)$, then difference it to get $(d_1, d_2, ...)$. Both $d_1$ and $d_2$ are calculated using $n_2$, so you've now introduced autocorrelation at lag 1.
Now look at what happens at that lag 1. $n_2$ is used to calculate $d_1$ and $d_2$, once subtracting from and once being subtracted from. [Begin I'm-way-in-over-my-head part.] In order for $d_1$ and $d_2$ to have the same sign, we'd need to have $n_1 < n_2$ and $n_2 < n_3$ (or vice versa), which is less likely than the alternatives, so we expect that the autocorrelation will be negative. [End I'm-way-in-over-my-head part, gasping for air.]