3

I have scan through all the similar topics and also read on Prof Rob J. Hyndman's ARIMAX muddle article.

Also, referencing to this, it is mentioned that a regression with ARIMA error is equivalent a differenced regression model with ARMA error.

As such, how do we interpret the coefficients once we did the differencing?: 

example:   
    library(fpp)
    data("insurance")
    fit <- auto.arima(insurance[,1], xreg=Advert[,1:2], d=0)
    Advert <- cbind(insurance[,2],
                    c(NA,insurance[1:39,2]),
                    c(NA,NA,insurance[1:38,2]),
                    c(NA,NA,NA,insurance[1:37,2]))
    colnames(Advert) <- paste("AdLag",0:3,sep="")
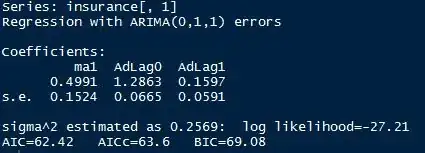
    fit <- auto.arima(insurance[,1], xreg=Advert[,1:2], d=1)

enter image description here

In this case, the error is ARIMA(0,1,1) and based from other answer as well as Prof Rob J. Hyndman's blog, we interpret it as per linear regression.

Therefore, is it right to interpret this as:

On average, 1 unit increase in tv advertisement this period leads to 1.2863 unit increase in insurance quotation, keeping other variables constant.

Equation: $Y_t = 1.2863X_t + 0.1597X_{t-1} + \eta_t$ where $\eta_t$ is ARIMA(0,1,1) error.

misosoup
  • 81
  • 7
  • In the last line, is it ARIMA(0,1,0) or (0,1,1)? Also, note that ARIMA and ARMA are spelled with all capital letters as they are acronyms. – Richard Hardy May 11 '17 at 11:33
  • Typo. So are the interpretations similar? – misosoup May 11 '17 at 14:46
  • Well, I have not looked at this carefully enough, so I would rather not mislead you by guessing whether this is correct or not. But +1 (from before already) as I am interested in the answer, too. – Richard Hardy May 11 '17 at 14:54
  • Assuming $X_t$ is fixed (deterministic) or stochastic but contemporaneously uncorrelated with $\eta_t$, i.e., $E(X_t\eta_t)=0$, then the coefficient $1.2863$ is the derivative of $Y_t$ with respect to $X_t$, $\frac{\partial Y_t}{\partial X_t} = 1.2863$. This agrees with you interpretation and, hence, I would say it is correct. – javlacalle May 13 '17 at 09:09
  • @javlacalle May i ask that when you say it is correct, it is regarding my interpretation with respect to the equation that i wrote, because i think i might have the wrong equation interpretation in the place (due to the differencing) :/ I will share some of my finding below – misosoup May 15 '17 at 02:53
  • I was referring to your sentence in bold, given your equation. The equation is correct, it agrees with [this post](https://stats.stackexchange.com/questions/110589/arima-with-xreg-rebuilding-the-fitted-values-by-hand). You may be also interested in [this post](https://stats.stackexchange.com/questions/141109/interpretation-of-arima-with-xreg-in-r/141159#141159) and the links therein. – javlacalle May 16 '17 at 08:29
  • @javlacalle i did an example using a tslm model (with first difference variables) and another using this (0,1,0) arima error model. I obtain the same coefficient. The 2 link you posted are for non differenced model. Hence we can interpret it directly. – misosoup May 19 '17 at 06:06
  • I did not check it carefully enough, but I think the specification of the model is correct. According to the source code (function `armafn` within `stats::arima`), the likelihood of the ARIMA model is evaluated for the original series minus the regressors times their the coefficients. – javlacalle May 19 '17 at 18:49

0 Answers0