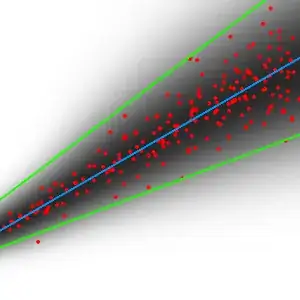
I want to perform linear regression on some data. For every value of x, the data values are distributed normally across y, around some mean. However, the variance increases linearly as x increases. I made this example graph:
Blue is the regression line, red are data points, black shows the normal distribution, and green visualizes the variance increasing.
How can I calculate a regression for the change in variance, while also performing a linear regression of the data? The data is heteroscedastic, and I've read up on methods for doing linear regression on such data. However, I haven't found anything on estimating the actual change in variance of the data.
I haven't studied stats rigorously, so any simple explanations or resources I could look at further would be appreciated.
More Details:
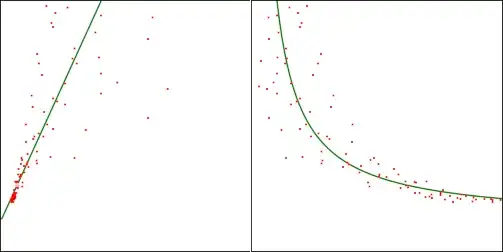
The original dataset follows $y = a/x + b$. The variance as $x$ changes follows a similar model $s^2 = c/x + d$. I transformed the data using $x' = 1/x$ to make the data linear (just to simplify the problem). Here is a sample graph (left is transformed, right is original):