4

With the upcoming French presidential election (first round on 23th of April 2017) many opinion polls are ordered and presented in the news. There are several initiatives to track the results of these polls, see Les Décodeurs or Wikipedia.

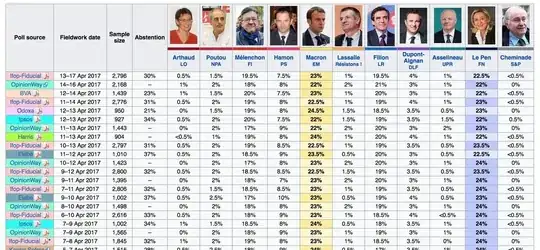
The following table sums up 20 most recent results for the 11 eleven candidates from polls published by 7 distinct poll offices:

Recent poll results

These polls display a remarkable consistency and the widest variation in the results series for a given candidate is of 2,5% over the last week. I find this form of consistency (used here in the layman sense!) very puzzling:

How likely is it that so many polls display such a high consistence?

I gathered a few facts about the methodology used and other conditions:

  • About $44$ millions ($44\times10^6$) are expected to vote.

  • Most offices recruit their sample via an Internet platform and reward the recruits (either with a tiny amount of money or a small gift). For instance, Opinion Way can reward recruits with 0,50€ (p.2, in French)

  • Some offices use rolling samples, where each day a sample of about 500 recruits is selected and whose answers are cumulated with the answers of the samples in the last days. The period concerned is documented by the “Fieldwork date” in the table. As you can see, these periods overlap (e.g. for Ifop-Fiducial at the top, the period for 11th-14th overlaps with the period for 13th-17th).

  • Offices work with the “méthode des quotas” which means that some variables (sex, age, social category, residence category and residence area), when observed on the sample, match closely the national statistics provided by the INSEE the National Institute of Statistics and Economic Studies in France.

  • Offices use several sample bias corrections, some of them being publicly alleged – e.g. the sample can be unbiased using poll results from the previous presidential election – some of them being “in-house” methods.

  • Poll results publication do not follow the standards of scientific publications, nevertheless the raw results must be communicated to a governmental instance built of judges (but not of statisticians) say.

  • Standard deviations are not provided. Many results however provide a margin of error table. See Opinion Way p. 4, Ipsos p. 3 or Ifop-Fiducial p. 3. These tables seem to assume that the standard deviation is given by $\sqrt{p(1-p)/N}$ where $p$ is the point estimate and $N$ the size of the sample. Cf. How do you decide the sample size when polling a large population? for the relation between margin of error for a 95% confidence interval and standard deviation.

Michaël Le Barbier
  • 151
  • 5
  • You state that pollsters aren't required to follow good scientific (statistical) practice, but I would think that most of them are associated in professional associations which ensure the adherence to certain standards (unless, of course, you consider polls also the "surveys" taken among callers of a talk show). The uniformity may be either because all companies use the same methods/corrections, or because they "correct" their results to get similar results to previously published polls...another possibility could be that the sampling error is very small, and thus all estimates are similar. – DeltaIV Apr 19 '17 at 09:51
  • @DeltaIV My wording is quite alluding so let me clarify what I meant: If we want to examine or criticise the results of a poll, we cannot access to a document describing the full experimental protocol and the derivations made to the final result – these are essentially considered as “business secrets”. Scientific publications are required to provide enough details for an export or group of experts (e.g. contributors to Cross Verified SE) to criticise the methods and the results. – Michaël Le Barbier Apr 19 '17 at 11:18
  • I understand. Do you have access to the standard errors, in addition to the point estimates? – DeltaIV Apr 19 '17 at 11:37
  • I do not, however the documentation of polls suggest a standard deviation of $\sqrt{p(1-p)/N}$, cf. my last edit. – Michaël Le Barbier Apr 19 '17 at 12:24
  • 1
    if with $p$ you mean $\hat{p}$ (the point estimate) then that's the Wald standard error. It's not very accurate (see https://stats.stackexchange.com/questions/62743/confidence-score-for-a-single-proportion?noredirect=1&lq=1 or many other similar questions on this site). I would have thought that pollsters would use more advanced estimation tools, introducing many corrections for nonresponse bias, stratification, etc. Anyway, if that's the formula they cite, you could try to add the SE to your table (you have the sample sizes) and make the check I suggested. – DeltaIV Apr 19 '17 at 14:59
  • @DeltaIV That's correct. Which check did you suggest? I overlooked that part. – Michaël Le Barbier Apr 19 '17 at 15:30
  • Compute the standard error SE for each estimate with your formula, use $\hat{p}\pm 1.96 SE$ to compute confidence intervals for each poll and see if the confidence intervals from different polls overlap (most of the times). – DeltaIV Apr 19 '17 at 15:38

0 Answers0