I'm assuming this is better explained in the 2nd edition of Simon's book (which should be out in a couple of days) as he and his students only worked out some of the theory for this years after Simon wrote his book.
What Marra & Wood (2011) showed was that if we want to do selection on a model with smooth terms, then one very good approach is to add an extra penalty to all the smooth terms. This additional penalty works with the smoothness penalty for that term to control both the wiggliness of the term and whether a term should be in the model at all.
So, unless you have any good theory to assume either smooth or linear/parametric forms/effects for the covariates, you could approach the problem as choosing among all models (representable by the additive combination of linear combinations of the basis functions) between one with smooths of each covariate all the way back to a model containing just an intercept.
For example:
library(mgcv)
data(trees)
ct1 <- gam(log(Volume) ~ s(Height) + s(Girth), data=trees, method = "REML", select = TRUE)
> summary(ct1)
Family: gaussian
Link function: identity
Formula:
log(Volume) ~ s(Height) + s(Girth)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.27273 0.01492 219.3 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(Height) 0.967 9 3.249 3.51e-06 ***
s(Girth) 2.725 9 75.470 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq.(adj) = 0.975 Deviance explained = 97.8%
-REML = -23.681 Scale est. = 0.0069012 n = 31
Looking at the output (specifically in the section Parametric coefficients), we note that both terms are highly significant.
But note the effective degrees of freedom value for the smooth of Height; it is ~1. What these tests are doing is explained in Wood (2013).
This suggests to me that Height should enter the model as a linear parametric term. We can evaluate this by plotting the fitted smooth:
> plot(ct1, select = 1, shade = TRUE, scale = 0, seWithMean = TRUE)
which gives:
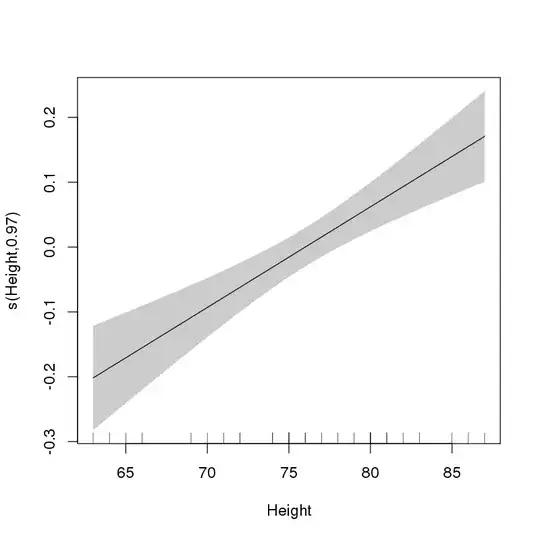
This clearly shows that the selected form of the effect of Height is linear.
However, if you didn't know this upfront (and you didn't because otherwise you wouldn't have asked the question) you can't now refit the model to these data using only a linear term for Height. That would cause you real problems with inference down the line. The output in summary() has accounted for the fact that you did this selection. If you refit the model with a linear parametric effect of Height, the output wouldn't know this and you'd get overly optimistic p-values.
As for question 2, as already mentioned in the comments, no, don't exponentiate the coefficients from this model. Also, don't delve into fitted models as the contents of these components is not always what you might expect. Use the extractor functions instead; in this case coef().
Later in the book when Simon gets to GLMs and GAMs, you'll see him model these data via a Gamma GLM:
ct1 <- gam(Volume ~ Height + s(Girth), data=trees, method = "REML",
family = Gamma(link = "log"))
In that model, because the fitting is being done on the scale of the linear predictor (on the log scale), the coefficients could be exponentiated to get some partial effect, but you are better off using predict(ct1, ...., type = "response") to get back fitted values/predictions on the scale of the response (in m^3).
Marra, G. & Wood, S. N. Practical variable selection for generalized additive models. Comput. Stat. Data Anal. 55, 2372–2387 (2011).
Wood, S. N. On p-values for smooth components of an extended generalized additive model. Biometrika 100, 221–228 (2013).
