5

Prediction of survival times in Cox proportional hazard regression model has been discussed here. In R, survfit::survival using the newdata argument gives a vector of estimated survival probabilities with a confidence interval.

The mathematical expression for a prediction is

$$\hat{h}_i(t) = \hat{h}_0(t) \exp(x_i' \hat{\beta}),$$

where $\hat{h}_0(t)$ the estimated baseline hazard and $\beta$ the Cox coefficient (for details, see link above). My question is how to find the mathematical expression for standard prediction error and prediction intervals for $\hat{h}_i(t)$.

R apparently knows a solution for this in its survfit function. I would like to understand how this works. I considered some survival analysis references but did not find an answer to this question. Here is an example:

library(survival)
fit <- coxph(Surv(futime, fustat) ~ age, data=ovarian) 
x_new <- data.frame(age = 60)
plot(survfit(fit, newdata=x_new))

enter image description here

Community
  • 1
tomka
  • 5,874
  • 3
  • 30
  • 71

1 Answers1

2

It's perhaps useful to note in your example that when age is taken to be the empirical mean, there is no difference in the plot.survfit output: e.g. plot(survfit(fit, newdata = data.frame(age=mean(ovarian$age)))) and plot(survfit(fit)) produce the same results. This is because the cox model using the hazard ratio to describe differences in survival between ovarian cancer patients of varying ages.

The survivor function is related to the hazard via:

$$S(T; x) = \exp \left\{ -\int_{0}^t \lambda_x (t)\right\} $$

or, according to the cox model specification:

$$S(T; x) = \exp \left\{ -\int_{0}^t \lambda_0 (t) \exp(X\beta)\right\} $$

Which can be written in terms of X and $\beta$ as a exponential modification to the empirical survivor function

$$S(T; x) = S_0(T) ^ {\exp(X\beta)} $$

If this is confusing it is easier to think of age as centered and scaled, $S_0$ is the unstratified survivor function, which does not vary based on $X$.

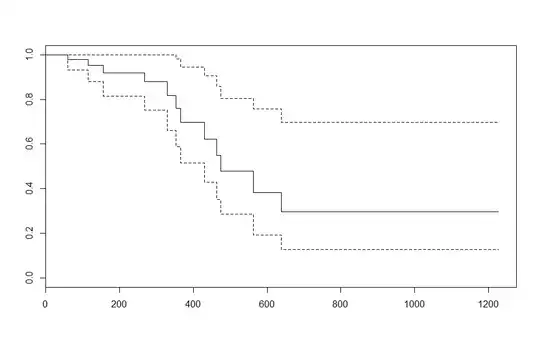
To verify this, the survival at 1,000 days is: 0.5204807. 60 is 3.834558 years above the mean age, resulting in a hazard ratio of $\exp(3.83\times 0.16) = 1.858$

Verifying this is the exponent, you find the 1,000 day survival for an ovarian cancer patient age 60 is tail(survfit(fit, newdata=x_new)$surv, 1) = 0.2971346 which equals: $0.5204807^{1.858}$.

That means that the issue of calculating the standard error for the "scaled" kaplan meier is just a delta method treating the survival curve and the coefficients as independent.

If $S(T, x) = S(T, 0) ^{\exp(\hat{\beta} X)}$ then

$$\text{var} \left( S(T, x) \right) \approx \frac{\partial S(T, x)}{\partial [S_0(T), \beta]} \left[ \begin{array}[cc]\ \text{var} \left(S_0(T) \right) & 0 \\ 0 & \text{var} \left(\hat{\beta} \right) \\ \end{array} \right] \frac{\partial S(T, x)}{\partial [S(T, 0), \beta]}^T $$

But as a note, calculation of bounds for the survivor function is still a huge area of research. I don't think this approach: using empirical bounds for the survivor function, takes adequate advantage of the proportional hazards assumption.

AdamO
  • 52,330
  • 5
  • 104
  • 209
  • Can you please clarify what is the difference between $S(T,0)$, $S_0(T)$ and $S(T_0)$? I think the first two are the same and last is maybe a typo? Also I think it would be great if you could elaborate a bit on how to obtain the gradient of $S(T,x)$ and the variance of $S(T_0)$. Thanks! – tomka Mar 20 '17 at 09:14
  • In a post on `r-help` the author of `survfit` comments that the delta method for $V(S)$ followed by normal theory confidence interval would be bad. He suggests using the standard error of the cummulative hazard, $- \log(S)$, instead. He does not specify how to arrive at this std error, but I believe the delta method applied to cummulative hazard in the same spirit as your equation may work. https://stat.ethz.ch/pipermail/r-help/2013-March/349567.html – tomka Mar 20 '17 at 11:56
  • @tomka good point. I think my answer can easily be modified to consider an appropriate transformation of $S_0(T)$ however. A choice which is used in Cox modeling is the complementary log-log link, which I think is the natural scale and log hazard ratios are additive on this scale which makes the $\delta$-method moot. – AdamO Mar 20 '17 at 14:05
  • @tomka I never used the notation $S(T_0)$. $S_0(T)$ is a "baseline" hazard function in a general sense. $S(T, 0)$ which could be better written as $S(T, X=0)$ is another way of expressing a baseline hazard function for a model which varies as a function of $X$. The key thing to realize about my answer vs. your question is that you refer to $\hat{h}_0(t)$ or an estimate of the baseline hazard function. We never actually obtain this: which *can* be estimated with smoothing/filtering. The method you use relates to the *empirical* survival function which does not rely on an estimate of $h_0(t)$ – AdamO Mar 20 '17 at 14:06
  • You do use $S(T_0)$ notation in the matrix. It is a typo I think and the baseline hazard is meant. I cannot suggest an edit because CV restricts edits to 6 characters minimum. – tomka Mar 20 '17 at 14:14
  • Regarding your last point, I believe we do obtain an estimator for $S(T,0)$ and `survfit` does so too internally. There are several estimators for example the Breslow estimator, which is default in `survfit`. My question is how `survfit` then arrives at the standard errors. I suppose a variance for the Breslow estimator is needed if the delta method is used. – tomka Mar 20 '17 at 14:25
  • @tomka Thanks for showing me the error! I've fixed this. An estimate of $S_0(T)$ is not the same as an estimate of $h_0(T)$ just as an estimate of a cumulative distribution function does not result in an estimate of the density. The former is estimable empirically whereas the latter requires smoothing / filtering. The survivor function is estimated *empirically* and *non-parametrically* by the Kaplan Meier and shifted by an independent and unrelated estimation technique of the Cox model. – AdamO Mar 20 '17 at 15:24