2

I'm trying to fit some data with linear regression like this:

Call:
lm(formula = time ~ nDOF:ndoms + I(nDOF^2):ndoms + I(1/nprocs^2):nDOF, 
    data = dataFact)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.077190 -0.007059  0.000202  0.006533  0.148240 

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)        -9.807e-03  2.123e-03  -4.619 6.57e-06 ***
nDOF:ndoms          3.441e-08  1.231e-09  27.963  < 2e-16 ***
ndoms:I(nDOF^2)     1.749e-12  8.741e-14  20.014  < 2e-16 ***
nDOF:I(1/nprocs^2)  1.103e-05  5.630e-07  19.586  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02039 on 220 degrees of freedom
Multiple R-squared:  0.9926,    Adjusted R-squared:  0.9925 
F-statistic:  9857 on 3 and 220 DF,  p-value: < 2.2e-16

As we can see, the fit is pretty good, but unfortunately, the smallest predicted values tend to be negative. enter image description here

Is there any way I could "shift" my model a little?

My attempt

I tried to solve the situation using generalized linear regression, like this

Call:
glm(formula = time ~ nDOF:ndoms + I(nDOF^2):ndoms + I(1/nprocs^2):nDOF, 
    family = gaussian(link = "log"), data = dataFact)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-0.19161  -0.07415  -0.04443   0.01376   0.23374  

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)        -2.550e+00  6.269e-02 -40.682  < 2e-16 ***
nDOF:ndoms          2.248e-07  1.582e-08  14.212  < 2e-16 ***
ndoms:I(nDOF^2)    -5.015e-12  9.254e-13  -5.420 1.57e-07 ***
nDOF:I(1/nprocs^2)  2.435e-05  3.958e-06   6.152 3.58e-09 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for gaussian family taken to be 0.006711178)

    Null deviance: 12.3909  on 223  degrees of freedom
Residual deviance:  1.4764  on 220  degrees of freedom
AIC: -479.25

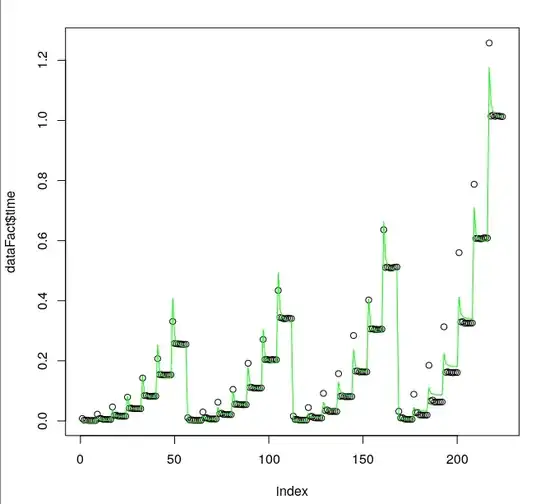
But as we can see, the plot is completely out

enter image description here

What am I doing wrong here? And is there any easy way to maintain the shape of the curve and just use GLM to predict only positive numbers?

My data

nprocs,nthreads,ndoms,size,nDOF,time

1,24,288,4,375,0.0946295
2,12,288,4,375,0.0641595
3,8,288,4,375,0.0599065
4,6,288,4,375,0.0549505
6,4,288,4,375,0.0538465
8,3,288,4,375,0.05184975
12,2,288,4,375,0.051091
24,1,288,4,375,0.0534245
1,24,288,6,1029,0.301089
2,12,288,6,1029,0.205296
3,8,288,6,1029,0.1908795
4,6,288,6,1029,0.1785225
6,4,288,6,1029,0.170867
8,3,288,6,1029,0.16909225
12,2,288,6,1029,0.169228
24,1,288,6,1029,0.1673835
1,24,288,8,2187,0.68576575
2,12,288,8,2187,0.49339725
3,8,288,8,2187,0.44999925
4,6,288,8,2187,0.4184415
6,4,288,8,2187,0.4006765
8,3,288,8,2187,0.39963125
12,2,288,8,2187,0.394082
24,1,288,8,2187,0.3925375
1,24,288,10,3993,1.32663875
2,12,288,10,3993,0.94414525
3,8,288,10,3993,0.87997
4,6,288,10,3993,0.816276
6,4,288,10,3993,0.78842875
8,3,288,10,3993,0.77410125
12,2,288,10,3993,0.7764705
24,1,288,10,3993,0.7638315
1,24,288,12,6591,2.2723285
2,12,288,12,6591,1.64944125
3,8,288,12,6591,1.52428725
4,6,288,12,6591,1.40552625
6,4,288,12,6591,1.3529915
8,3,288,12,6591,1.334635
12,2,288,12,6591,1.325433
24,1,288,12,6591,1.323585
1,24,288,14,10125,3.573002
2,12,288,14,10125,2.588366
3,8,288,14,10125,2.42213025
4,6,288,14,10125,2.23624525
6,4,288,14,10125,2.14378325
8,3,288,14,10125,2.1225845
12,2,288,14,10125,2.11212025
24,1,288,14,10125,2.1014935
1,24,288,16,14739,5.3447225
2,12,288,16,14739,3.8467885
3,8,288,16,14739,3.627996
4,6,288,16,14739,3.3243295
6,4,288,16,14739,3.2092895
8,3,288,16,14739,3.16907825
12,2,288,16,14739,3.1560615
24,1,288,16,14739,3.12689
1,24,384,4,375,0.115369
2,12,384,4,375,0.0803815
3,8,384,4,375,0.0763355
4,6,384,4,375,0.07056225
6,4,384,4,375,0.0682565
8,3,384,4,375,0.07106375
12,2,384,4,375,0.06758
24,1,384,4,375,0.07009675
1,24,384,6,1029,0.3517015
2,12,384,6,1029,0.26008075
3,8,384,6,1029,0.2434895
4,6,384,6,1029,0.229354
6,4,384,6,1029,0.222431
8,3,384,6,1029,0.22455025
12,2,384,6,1029,0.22294525
24,1,384,6,1029,0.21949025
1,24,384,8,2187,0.814259
2,12,384,8,2187,0.6097535
3,8,384,8,2187,0.579098
4,6,384,8,2187,0.54244075
6,4,384,8,2187,0.5272745
8,3,384,8,2187,0.532494
12,2,384,8,2187,0.52172925
24,1,384,8,2187,0.52157525
1,24,384,10,3993,1.5572355
2,12,384,10,3993,1.197648
3,8,384,10,3993,1.1347285
4,6,384,10,3993,1.056746
6,4,384,10,3993,1.02914675
8,3,384,10,3993,1.01935525
12,2,384,10,3993,1.02304
24,1,384,10,3993,1.01973325
1,24,384,12,6591,2.6899245
2,12,384,12,6591,2.06899875
3,8,384,12,6591,1.95328225
4,6,384,12,6591,1.83718875
6,4,384,12,6591,1.79995825
8,3,384,12,6591,1.7651285
12,2,384,12,6591,1.7616405
24,1,384,12,6591,1.7832275
1,24,384,14,10125,4.24194525
2,12,384,14,10125,3.25947975
3,8,384,14,10125,3.102823
4,6,384,14,10125,2.910768
6,4,384,14,10125,2.84159925
8,3,384,14,10125,2.812863
12,2,384,14,10125,2.79452
24,1,384,14,10125,2.783541
1,24,384,16,14739,6.34359525
2,12,384,16,14739,4.87417475
3,8,384,16,14739,4.68763775
4,6,384,16,14739,4.409049
6,4,384,16,14739,4.225499
8,3,384,16,14739,4.19000525
12,2,384,16,14739,4.1685855
24,1,384,16,14739,4.13447625
1,24,576,4,375,0.149258
2,12,576,4,375,0.11306475
3,8,576,4,375,0.1106305
4,6,576,4,375,0.10277875
6,4,576,4,375,0.10034075
8,3,576,4,375,0.09992475
12,2,576,4,375,0.100055
24,1,576,4,375,0.1013415
1,24,576,6,1029,0.4631635
2,12,576,6,1029,0.363534
3,8,576,6,1029,0.346867
4,6,576,6,1029,0.33634225
6,4,576,6,1029,0.327822
8,3,576,6,1029,0.32915075
12,2,576,6,1029,0.325756
24,1,576,6,1029,0.3244965
1,24,576,8,2187,1.0745575
2,12,576,8,2187,0.8715855
3,8,576,8,2187,0.8237175
4,6,576,8,2187,0.7936485
6,4,576,8,2187,0.78037075
8,3,576,8,2187,0.78318125
12,2,576,8,2187,0.7757685
24,1,576,8,2187,0.769712
1,24,576,10,3993,2.0662435
2,12,576,10,3993,1.69664675
3,8,576,10,3993,1.61632025
4,6,576,10,3993,1.55593225
6,4,576,10,3993,1.52227825
8,3,576,10,3993,1.52255425
12,2,576,10,3993,1.51433725
24,1,576,10,3993,1.5073515
1,24,576,12,6591,3.55465175
2,12,576,12,6591,2.9219815
3,8,576,12,6591,2.813871
4,6,576,12,6591,2.688473
6,4,576,12,6591,2.642868
8,3,576,12,6591,2.62695125
12,2,576,12,6591,2.62418275
24,1,576,12,6591,2.63111275
1,24,576,14,10125,5.62003375
2,12,576,14,10125,4.66024075
3,8,576,14,10125,4.45642925
4,6,576,14,10125,4.269482
6,4,576,14,10125,4.20735775
8,3,576,14,10125,4.180191
12,2,576,14,10125,4.1697685
24,1,576,14,10125,4.17519025
1,24,576,16,14739,8.412904
2,12,576,16,14739,6.920983
3,8,576,16,14739,6.62266525
4,6,576,16,14739,6.36904225
6,4,576,16,14739,6.2505475
8,3,576,16,14739,6.21563775
12,2,576,16,14739,6.198577
24,1,576,16,14739,6.17604925
1,24,1152,4,375,0.26259325
2,12,1152,4,375,0.21321625
3,8,1152,4,375,0.20502075
4,6,1152,4,375,0.19962325
6,4,1152,4,375,0.1968235
8,3,1152,4,375,0.19961675
12,2,1152,4,375,0.20011775
24,1,1152,4,375,0.19877925
1,24,1152,6,1029,0.79873425
2,12,1152,6,1029,0.69796225
3,8,1152,6,1029,0.67075925
4,6,1152,6,1029,0.6483425
6,4,1152,6,1029,0.648511
8,3,1152,6,1029,0.64445625
12,2,1152,6,1029,0.6470985
24,1,1152,6,1029,0.63747875
1,24,1152,8,2187,1.84742675
2,12,1152,8,2187,1.624627
3,8,1152,8,2187,1.5797865
4,6,1152,8,2187,1.5516275
6,4,1152,8,2187,1.53921525
8,3,1152,8,2187,1.53861475
12,2,1152,8,2187,1.5321545
24,1,1152,8,2187,1.520184
1,24,1152,10,3993,3.5739245
2,12,1152,10,3993,3.15653825
3,8,1152,10,3993,3.120543
4,6,1152,10,3993,3.0330285
6,4,1152,10,3993,3.0156615
8,3,1152,10,3993,3.00419675
12,2,1152,10,3993,2.995779
24,1,1152,10,3993,2.9914245
1,24,1152,12,6591,6.14267725
2,12,1152,12,6591,5.5148995
3,8,1152,12,6591,5.35443675
4,6,1152,12,6591,5.25097775
6,4,1152,12,6591,5.26166925
8,3,1152,12,6591,5.1859525
12,2,1152,12,6591,5.21059225
24,1,1152,12,6591,5.17157525
1,24,1152,14,10125,9.910901
2,12,1152,14,10125,8.696456
3,8,1152,14,10125,8.519928
4,6,1152,14,10125,8.34710125
6,4,1152,14,10125,8.30145125
8,3,1152,14,10125,8.23857
12,2,1152,14,10125,8.28954975
24,1,1152,14,10125,8.22843225
1,24,1152,16,14739,14.4608565
2,12,1152,16,14739,12.976403
3,8,1152,16,14739,12.6674635
4,6,1152,16,14739,12.430683
6,4,1152,16,14739,12.319599
8,3,1152,16,14739,12.27644125
12,2,1152,16,14739,12.2994265
24,1,1152,16,14739,12.2351635
Eenoku
  • 443
  • 8
  • 17
  • You can, of course, always add a constant such that your predictions are always at least 0. But then your regression will not be the one that minimizes the quadratic errors! If you need to impose boundedness on the predictions, as you already mentioned, you need to specify a different model other than linear, and this will depend on what your data is. Maybe a left-censored tobit is what you need? – Anna SdTC Mar 14 '17 at 08:55
  • In principle a log link ensures positive predictions (and in my view is a much better solution than Tobit). What's missing from this, so far as I can see, is a record of how you calculated the predicted values shown on the graph. Also, in a situation where there are several predictors an index plot is often less helpful than a plot of observed and predicted responses. Otherwise this question seems to be asking what is wrong with your R code that you don't see the results you expect, and that would be off-topic here. Please see advice in the Help Center on software-specific suggestions. – Nick Cox Mar 14 '17 at 09:05
  • Your initial multiple regression model seems to be doing quite well **in terms of predictive accuracy**: adjusted $R^2$ is above .99 with 220 degrees of freedom. Other metrics such as cross-validation error or AIC would be more suitable to estimate generalization error, but in this case it looks like the only issue are the 6 data point with index $i>150$ where you're underestimating the response. **However**, your model is a bit weird in that only some very specific interaction terms are present, and no main effects. Did you get to this model by means of stepwise regression? [1/2] – DeltaIV Mar 14 '17 at 09:43
  • [1/2] If this is the case, then the adjusted $R^2$ may well be meaningless, and the model could have no predictive ability at all. If not, constrained linear regression (which doesn't mean to just add a constant so that your model is shifted away from zero) could solve your problem. Please explain how you arrived at the first model. – DeltaIV Mar 14 '17 at 09:45
  • @DeltaIV I've ommited main effects because of t-tests - they seemed to have no singificant effect to the model. Cross-validation seems ok. I'll add more details in the evening, thank you for your response. – Eenoku Mar 14 '17 at 10:12
  • 3
    omitting main effects because of t-tests is exactly what you shouldn't have done. Now the adjusted $R^2$ is unreliable, and cross validation will **only** be reliable if, for each fold, you repeat from scratch the variable selection process. If you just omit the main effects once and for all, based on the full training set, and then you compute the cross-validation error of this selected model, the number you get is mumbo-jumbo just as the current adjusted $R^2$. It *might* be that your model is actually good, but you cannot say that based on these metrics. – DeltaIV Mar 14 '17 at 10:41
  • 2
    PS also, omitting main effects when only interactions are significant goes against the hierarchical principle. Many good answers on this site - check [this one](http://stats.stackexchange.com/questions/27724/do-all-interactions-terms-need-their-individual-terms-in-regression-model) for example. – DeltaIV Mar 14 '17 at 10:43

1 Answers1

3

Given the way you derived your model (removing terms based on $t$-tests, without even taking into account the hierarchical principle), model intepretation and inference based on this model are already invalid. At this point, I don't think you would make the situation much worse it you just bounded it above zero. Something like 

model <- lm(formula = time ~ nDOF:ndoms + I(nDOF^2):ndoms + I(1/nprocs^2):nDOF, data = dataFact)

dirty_trick <- function(newdata, model){
    yhat <- predict(model, newdata)
    yhat <- max(0, yhat)
}

where newdata is the dataframe containing the points where you want to make predictions. You can use the dirty_trick function to get nonnegative predictions at points newdata based on your model. You could easily modify dirty_trick to return an (invalid) upper confidence interval (the lower one is obviously 0) alongside with the point estimate, but since the confidence interval is indeed invalid, I omitted that.

I stress once again that this model is both:

  • hard to interpret, because, since you removed the main effects but left the interactions in, the interactions are probably "catching up" whatever influence the main effects had on the response
  • likely to lead to false inference, because your standard errors, confidence intervals, $p$-values, adjusted $R^2$, etc. are computed without taking into account the selection process.

Thus I strongly suggest that you use it only for prediction, and only after having tested its predictive accuracy on data not used for fitting (or using cross-validation, BUT only if you repeat the variables selection step in each fold).

DeltaIV
  • 15,894
  • 4
  • 62
  • 104