I have a following generalised linear model with logarithm link function in R
Call:
glm(formula = time ~ I(1/nprocs) + nDOF + I(nDOF^2) + ndoms +
nDOF:ndoms + I(nDOF^2):ndoms + I(nDOF^3):ndoms, family = gaussian(link = "log"),
data = dataFact)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.98297 -0.14332 -0.09090 0.02355 1.09854
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.148e+00 1.811e-01 -11.861 < 2e-16 ***
I(1/nprocs) 6.319e-02 1.487e-02 4.250 3.18e-05 ***
nDOF 4.038e-04 3.476e-05 11.615 < 2e-16 ***
I(nDOF^2) -1.154e-08 1.575e-09 -7.325 4.68e-12 ***
ndoms 8.157e-04 2.178e-04 3.746 0.00023 ***
nDOF:ndoms 2.678e-07 5.918e-08 4.525 9.96e-06 ***
I(nDOF^2):ndoms -3.270e-11 5.757e-12 -5.680 4.32e-08 ***
ndoms:I(nDOF^3) 1.174e-15 1.932e-16 6.075 5.53e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for gaussian family taken to be 0.1183373)
Null deviance: 3891.805 on 223 degrees of freedom
Residual deviance: 25.561 on 216 degrees of freedom
AIC: 167.48
Number of Fisher Scoring iterations: 5
I want to use it as a predictive model, so I'd like to evaluate two main criteria:
- goodness of fit on the whole train data set
- "goodness of prediction" by 10-fold cross-validation
I'd like to have some argument (together with some "rule of thumb"), so that I could say, that my model is "good enough", not only that it's better than some other model (which I can say now considering AIC).
Fit on the whole training data set
1st attempt
I considered using Nagelkerke pseudo-R2, but I'm not sure, if it's compatible with my GLM model (gaussian family, but logarithm link function).
Moreover, I'm worried about its "performance" on larger data sets (about 10000 observations), where the formula has a lot of terms.
Pseudo-R2 for my fit looks like this:
Nagelkerke R2:
$N
[1] 224
$R2
[1] 1
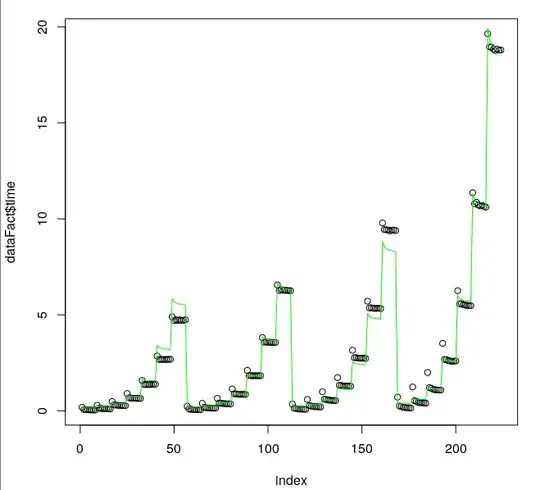
As we can see from plots, while the fit is pretty good, it's definitely not perfect, so I'd expect R2 about 0.98, not 1.
2nd attempt
I thought about the interpretation of Null and residual deviance. I know, that residual deviance tells me about the improvement of the "null model" by my formula, but I'm not able to interpret it as the absolute value, so I could say, that the improvement is good enough.
I found following formula (in this answer), but I don't know if it's correct to interpret its result in the way "when this number is larger than 0.9, then my model is ok".
1 - (Residual Deviance/Null Deviance)
Goodness of prediction by 10-fold cross-validation
Here I'm trying to perform 10 iterations of cross-validation and store RMSE in every iteration, so I can compute its mean and standard deviation (like it was recommended in this answer).
The result looks like this:
mean(RMSE)=0.367754, sd(RMSE)=0.076150
My problem is, again, the interpretation - how can I say, that those numbers are good enough for the model to be considered well-predicting or otherwise?
Plots of fit on the whole training data set
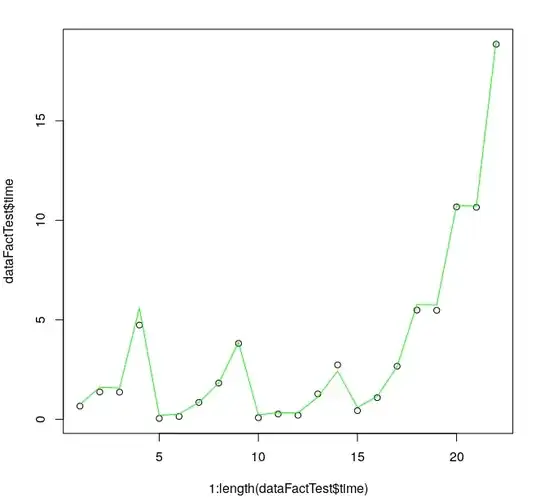
Examples of plots of cross-validation
Data set
nprocs,nthreads,ndoms,size,nDOF,time
1,24,288,4,375,0.17715325
2,12,288,4,375,0.0629865
3,8,288,4,375,0.057708125
4,6,288,4,375,0.04788125
6,4,288,4,375,0.04303875
8,3,288,4,375,0.04060275
12,2,288,4,375,0.038032625
24,1,288,4,375,0.034977375
1,24,288,6,1029,0.284978625
2,12,288,6,1029,0.13397875
3,8,288,6,1029,0.125101
4,6,288,6,1029,0.110273375
6,4,288,6,1029,0.105055625
8,3,288,6,1029,0.10273
12,2,288,6,1029,0.100959875
24,1,288,6,1029,0.099074375
1,24,288,8,2187,0.479892
2,12,288,8,2187,0.306054125
3,8,288,8,2187,0.295369625
4,6,288,8,2187,0.284210125
6,4,288,8,2187,0.273315125
8,3,288,8,2187,0.274951375
12,2,288,8,2187,0.266159875
24,1,288,8,2187,0.263813125
1,24,288,10,3993,0.89622025
2,12,288,10,3993,0.673204
3,8,288,10,3993,0.666580625
4,6,288,10,3993,0.6477035
6,4,288,10,3993,0.648032125
8,3,288,10,3993,0.64495625
12,2,288,10,3993,0.640551125
24,1,288,10,3993,0.638785875
1,24,288,12,6591,1.580801
2,12,288,12,6591,1.37637042857
3,8,288,12,6591,1.36346242857
4,6,288,12,6591,1.36495214286
6,4,288,12,6591,1.36805057143
8,3,288,12,6591,1.36849742857
12,2,288,12,6591,1.37384785714
24,1,288,12,6591,1.37941357143
1,24,288,14,10125,2.84967157143
2,12,288,14,10125,2.66627714286
3,8,288,14,10125,2.682575
4,6,288,14,10125,2.66889842857
6,4,288,14,10125,2.677353
8,3,288,14,10125,2.67224042857
12,2,288,14,10125,2.68130785714
24,1,288,14,10125,2.67892771429
1,24,288,16,14739,4.89139571429
2,12,288,16,14739,4.69489785714
3,8,288,16,14739,4.74105342857
4,6,288,16,14739,4.70664585714
6,4,288,16,14739,4.73917842857
8,3,288,16,14739,4.70832771429
12,2,288,16,14739,4.715311
24,1,288,16,14739,4.736754
1,24,384,4,375,0.23214775
2,12,384,4,375,0.085062
3,8,384,4,375,0.0773935
4,6,384,4,375,0.063308375
6,4,384,4,375,0.056720375
8,3,384,4,375,0.053515875
12,2,384,4,375,0.050725
24,1,384,4,375,0.047851875
1,24,384,6,1029,0.387123125
2,12,384,6,1029,0.177154
3,8,384,6,1029,0.164021375
4,6,384,6,1029,0.1471485
6,4,384,6,1029,0.13990975
8,3,384,6,1029,0.136657
12,2,384,6,1029,0.13419125
24,1,384,6,1029,0.13110525
1,24,384,8,2187,0.646564875
2,12,384,8,2187,0.403944
3,8,384,8,2187,0.393314375
4,6,384,8,2187,0.37626875
6,4,384,8,2187,0.368974375
8,3,384,8,2187,0.358301
12,2,384,8,2187,0.359731125
24,1,384,8,2187,0.3541595
1,24,384,10,3993,1.135393
2,12,384,10,3993,0.884951625
3,8,384,10,3993,0.879945
4,6,384,10,3993,0.855973375
6,4,384,10,3993,0.8522425
8,3,384,10,3993,0.852744375
12,2,384,10,3993,0.855075875
24,1,384,10,3993,0.8507125
1,24,384,12,6591,2.10579685714
2,12,384,12,6591,1.83842342857
3,8,384,12,6591,1.83237142857
4,6,384,12,6591,1.82270728571
6,4,384,12,6591,1.82788628571
8,3,384,12,6591,1.82526614286
12,2,384,12,6591,1.82717142857
24,1,384,12,6591,1.82618185714
1,24,384,14,10125,3.81616642857
2,12,384,14,10125,3.56664771429
3,8,384,14,10125,3.58948371429
4,6,384,14,10125,3.56408085714
6,4,384,14,10125,3.56926157143
8,3,384,14,10125,3.55938014286
12,2,384,14,10125,3.55807242857
24,1,384,14,10125,3.55977614286
1,24,384,16,14739,6.55986157143
2,12,384,16,14739,6.26693228571
3,8,384,16,14739,6.30919285714
4,6,384,16,14739,6.27896728571
6,4,384,16,14739,6.27579871429
8,3,384,16,14739,6.27007928571
12,2,384,16,14739,6.26270857143
24,1,384,16,14739,6.25499785714
1,24,576,4,375,0.346824
2,12,576,4,375,0.127150875
3,8,576,4,375,0.11508025
4,6,576,4,375,0.097335
6,4,576,4,375,0.083914125
8,3,576,4,375,0.080992125
12,2,576,4,375,0.075828625
24,1,576,4,375,0.070827625
1,24,576,6,1029,0.59015625
2,12,576,6,1029,0.26846175
3,8,576,6,1029,0.245241875
4,6,576,6,1029,0.2193675
6,4,576,6,1029,0.208428375
8,3,576,6,1029,0.207515
12,2,576,6,1029,0.204429
24,1,576,6,1029,0.197228
1,24,576,8,2187,0.98994575
2,12,576,8,2187,0.605623
3,8,576,8,2187,0.587526875
4,6,576,8,2187,0.55606225
6,4,576,8,2187,0.546602
8,3,576,8,2187,0.537873375
12,2,576,8,2187,0.536193625
24,1,576,8,2187,0.527466375
1,24,576,10,3993,1.725655375
2,12,576,10,3993,1.325127375
3,8,576,10,3993,1.317314625
4,6,576,10,3993,1.290353
6,4,576,10,3993,1.285149
8,3,576,10,3993,1.283298375
12,2,576,10,3993,1.283781375
24,1,576,10,3993,1.2788885
1,24,576,12,6591,3.15235257143
2,12,576,12,6591,2.765567
3,8,576,12,6591,2.76951185714
4,6,576,12,6591,2.74102728571
6,4,576,12,6591,2.737753
8,3,576,12,6591,2.73729985714
12,2,576,12,6591,2.73825257143
24,1,576,12,6591,2.72781542857
1,24,576,14,10125,5.71093614286
2,12,576,14,10125,5.35875985714
3,8,576,14,10125,5.36633285714
4,6,576,14,10125,5.34668342857
6,4,576,14,10125,5.32762214286
8,3,576,14,10125,5.33975814286
12,2,576,14,10125,5.350373
24,1,576,14,10125,5.31987557143
1,24,576,16,14739,9.78473642857
2,12,576,16,14739,9.44161628571
3,8,576,16,14739,9.42669171429
4,6,576,16,14739,9.41840128571
6,4,576,16,14739,9.37364014286
8,3,576,16,14739,9.41561828571
12,2,576,16,14739,9.41685542857
24,1,576,16,14739,9.39101542857
1,24,1152,4,375,0.710592875
2,12,1152,4,375,0.246370625
3,8,1152,4,375,0.2160605
4,6,1152,4,375,0.182422125
6,4,1152,4,375,0.164191875
8,3,1152,4,375,0.1583665
12,2,1152,4,375,0.1544865
24,1,1152,4,375,0.142128
1,24,1152,6,1029,1.2401235
2,12,1152,6,1029,0.52502025
3,8,1152,6,1029,0.490228
4,6,1152,6,1029,0.43791025
6,4,1152,6,1029,0.419299125
8,3,1152,6,1029,0.411805375
12,2,1152,6,1029,0.4083735
24,1,1152,6,1029,0.39699275
1,24,1152,8,2187,1.993820125
2,12,1152,8,2187,1.204231625
3,8,1152,8,2187,1.166492625
4,6,1152,8,2187,1.116419625
6,4,1152,8,2187,1.092001625
8,3,1152,8,2187,1.0832535
12,2,1152,8,2187,1.076723875
24,1,1152,8,2187,1.0744375
1,24,1152,10,3993,3.511545625
2,12,1152,10,3993,2.66910925
3,8,1152,10,3993,2.66473925
4,6,1152,10,3993,2.60924175
6,4,1152,10,3993,2.594369125
8,3,1152,10,3993,2.578603625
12,2,1152,10,3993,2.581412625
24,1,1152,10,3993,2.594349375
1,24,1152,12,6591,6.256258375
2,12,1152,12,6591,5.568122625
3,8,1152,12,6591,5.583774125
4,6,1152,12,6591,5.523111625
6,4,1152,12,6591,5.503487125
8,3,1152,12,6591,5.48894275
12,2,1152,12,6591,5.4785635
24,1,1152,12,6591,5.473963875
1,24,1152,14,10125,11.3590212857
2,12,1152,14,10125,10.7868857143
3,8,1152,14,10125,10.8603297143
4,6,1152,14,10125,10.7189155714
6,4,1152,14,10125,10.6728481429
8,3,1152,14,10125,10.695908
12,2,1152,14,10125,10.6502984286
24,1,1152,14,10125,10.6126634286
1,24,1152,16,14739,19.6414048571
2,12,1152,16,14739,18.9570958571
3,8,1152,16,14739,18.950933
4,6,1152,16,14739,18.8408438571
6,4,1152,16,14739,18.7679364286
8,3,1152,16,14739,18.848793
12,2,1152,16,14739,18.7847892857
24,1,1152,16,14739,18.8019534286