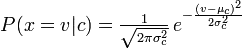I have seen a few times the technique of using the Gaussian PDF for continuous features in Naive Bayes. here and here. Illustrated in the first link:
How is this possible? I always learnt that the PDF is not a probability -- as the probability of any exact value of x is zero.
You're right that the statement is wrong. It should be a likelihood:
$$L(c \mid x=v)=\frac{1}{\sqrt{2\pi\sigma_c^2}}e^{-\frac{(v-\mu_c)^2}{2\sigma_c^2}}$$
A likelihood applies here because we are interested in the relative likelihood that a point belongs to each class:
$$P(c=c' \mid x=v) = \frac{L(c=c' \mid x=v)}{\sum_{c_i} L(c=c_i \mid x=v)}.$$
If you're interested in a lengthy and rigorous explanation check this out. To summarize, it all comes down to integral approximations. To get the probability of a specific variable value from the variable's continuous probability density function (PDF), you integrate the PDF around the value in question over an interval of width epsilon, and take the limit of that integral as epsilon approaches 0. For small epsilon, this integral will be equivalent to the product of epsilon and the height of the PDF at the variable value in question. Ordinarily, the limit of this expression would be to 0 as epsilon approached 0. However, as Neil mentioned in his answer, in the case of Naive Bayes we are interested in the ratio of conditional probabilities. Because both the numerator and denominator of our ratio will include a factor of epsilon, these factors of epsilon cancel out. As a result, the limit of the ratio of conditional probabilities will be equivalent to the ratio of the PDF heights at the variable value in question.
