5

Michaelis Menten Function Lineweaver Burk Plot

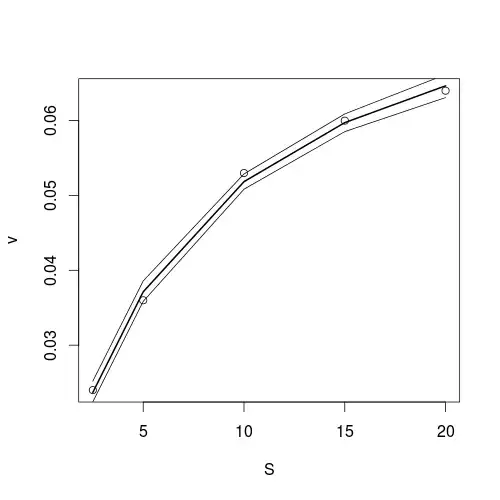
Okay, so the kinetics of enzymatic velocity of catalysis with a substrate is usually measured with a hyperbolic model known as the Michaelis Menten model. That is, v = (VMax * [S]) / ([S] + KM), where "KM = one-half the substrate concentration at VMax, and VMax is the expected upper plateau of the hyperbola.

So I have a nonlinear regression model and I want the 95% confidence bands accounting for the standard errors. How do I get that? 

S = c(2.5, 5.0, 10.0, 15.0, 20.0)
v = c(0.024, 0.036, 0.053, 0.060, 0.064)
mm <- data.frame(cbind(S,v))
#View(mm)
mm

S v
1 2.5 0.024
2 5.0 0.036
3 10.0 0.053
4 15.0 0.060
5 20.0 0.064

plot(v ~ S, data = mm, main = "Michealis Menten Nonlinear Regression Fitting", 
     xlab = "Substrate Concentration (mM)", ylab = "Rate (mM / sec)", 
     cex.lab = 1.4, cex.main = 1, pch = 16)

model <- nls(v ~ S*Vm/(S + K), data = mm, start = list(K = max(mm$v)/2, Vm = max(mm$v)))
summary(model)
#----
Formula: v ~ S * Vm/(S + K)

Parameters:
Estimate Std. Error t value Pr(>|t|) 
K 6.561892 0.478720 13.71 0.00084 ***
Vm 0.085857 0.002353 36.49 4.52e-05 ***
---
Signif. codes: 
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.001035 on 3 degrees of freedom

Number of iterations to convergence: 6 
Achieved convergence tolerance: 2.298e-06

curve(x * 0.085857 /(x + 6.561892), col = "darkorchid3", add = TRUE)

I've also double reciprocal LineWeaver Burk Model for calculating VMax & KM with linear regression. But in my opinion, the nonlinear regression model computes the parameters better. 

mm$Reciprocal_S <- 1 / mm$S
mm$Reciprocal_v <- 1 / mm$v
mm
#---------
S v Reciprocal_S Reciprocal_v
1 2.5 0.024 0.40000000 41.66667
2 5.0 0.036 0.20000000 27.77778
3 10.0 0.053 0.10000000 18.86792
4 15.0 0.060 0.06666667 16.66667
5 20.0 0.064 0.05000000 15.62500
#-----
plot(Reciprocal_v ~ Reciprocal_S, data = mm, pch = 16, xlab = "(1 / [S])", ylab = "(1 / v)",
     cex.main = 2, cex.lab = 1.4, main = "Experimental Lineweaver Burk Plot")

linear_model <- lm(mm$Reciprocal_v ~ mm$Reciprocal_S)
summary(linear_model)
#--------
Call:
lm(formula = mm$Reciprocal_v ~ mm$Reciprocal_S)

Residuals:
1 2 3 4 5 
-0.30625 0.89115 -0.47556 -0.16243 0.05309

Coefficients:
Estimate Std. Error t value Pr(>|t|) 
(Intercept) 11.8003 0.4449 26.53 0.000118 ***
mm$Reciprocal_S 75.4314 2.1357 35.32 4.99e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.6173 on 3 degrees of freedom
Multiple R-squared: 0.9976, Adjusted R-squared: 0.9968 
F-statistic: 1248 on 1 and 3 DF, p-value: 4.991e-05
#-----
 abline(linear_model)

Now how do I get the 95% confidence bands for this meaningful biochemical model, the hyperbolic one?

xyz123
  • 185
  • 1
  • 7
  • 2
    This is really a methods/theory question rather than a coding question. After you resolve your current lack of an algorithm, then it will become a fairly easy coding question. – DWin Feb 28 '17 at 18:15
  • I want R to make the model so I think it's a coding question. How do you think I made the hyperbola? With the nls R function. –  Feb 28 '17 at 18:16
  • 3
    I agree with @42-. It's unclear on what method you want to use to calculate confidence intervals. You need some modeling assumption. Just because you want to do this in R doesn't make it a coding question. You still at the part where you don't know *what* to do, not *how* to do it. There are no magic CI functions in stats that work for everything. – MrFlick Feb 28 '17 at 18:23
  • This question could be improved with an explanation of how standard error and confidence are typically calculated for the Michales Menten model. Experienced R programmers may not be familiar with this particular model, but could likely help you implement the algorithm you want to use if you describe it clearly. – Joe Feb 28 '17 at 18:28
  • 1
    First of all, whether Lineweaver-Burk or the non-linear fit is better depends on the uncertainty strukture. You should examine the residuals carefully. Anyway, I'd bootstrap the predictions. – Roland Feb 28 '17 at 18:30
  • Right, I suppose I just assumed that adding confidence bands to a hyperbolic function should be roughly as difficult as adding error bars to a linear regression model. I suppose I have underestimated the scope of the problem. –  Feb 28 '17 at 18:35
  • The second method (which I think might be called "linearization by exchange of variables") appears similar to that used by @w_huber in: http://stats.stackexchange.com/questions/247709/reliability-of-a-fitted-curve/247885#247885 . My experience is that answers by w_huber are high quality and this one had the added advantage that it was expressed in R. – DWin Feb 28 '17 at 19:48

1 Answers1

5

I think the propagate package can do what you are looking for.

require(propagate)

pred_model <- predictNLS(model, newdata=mm)
conf_model <- pred$summary
plot(v~S)

lines(conf_model$Prop.Mean.1 ~ S, lwd=2)
lines(conf_model$"Sim.2.5%" ~ S, lwd=1)
lines(conf_model$"Sim.97.5%" ~ S, lwd=1)

enter image description here

Robbie
  • 407
  • 4
  • 15
  • Wow! Thank you very much. I like to see that the points are within the confidence intervals. I wonder why the main hyperbola has lost its curve, though. It seems to come to a few points. – xyz123 Mar 01 '17 at 07:41