Conditional expectation of a truncated RV derivation, gumbel distribution (logistic difference)

Question

I have two random variables which are independent and identically distributed, i.e. $\epsilon_{1}, \epsilon_{0} \overset{\text{iid}}{\sim} \text{Gumbel}(\mu,\beta)$:

$$F(\epsilon) = \exp(-\exp(-\frac{\epsilon-\mu}{\beta})),$$

$$f(\epsilon) = \dfrac{1}{\beta}\exp(-\left(\frac{\epsilon-\mu}{\beta}+\exp(-\frac{\epsilon-\mu}{\beta})\right)).$$

I am trying to calculate two quantities:

1. $$\mathbb{E}_{\epsilon_{1}}\mathbb{E}_{\epsilon_{0}|\epsilon_{1}}\left[c+\epsilon_{1}|c+\epsilon_{1}>\epsilon_{0}\right]$$
2. $$\mathbb{E}_{\epsilon_{1}}\mathbb{E}_{\epsilon_{0}|\epsilon_{1}}\left[\epsilon_{0}|c+\epsilon_{1}<\epsilon_{0}\right]$$

I get to a point where I need to do integration on something of the form: $e^{e^{x}}$, which seems to not have an integral in closed form. Can anyone help me out with this? Maybe I have done something wrong.

I feel there definitely should be closed form solution. (EDIT: Even if it is not closed form, but there would be software to quickly evaluate the integral [such as Ei(x)], that would be ok I suppose.)

---

EDIT:

I think with a change of variables, let

$$y =\exp(-\frac{\epsilon_{1}-\mu}{\beta})$$ and

$$\mu-\beta\ln y =\epsilon_{1}$$

This maps to $[0,\;\infty)$ and $\left[0,\;\exp(-\frac{\epsilon_{0}-c-\mu}{\beta})\right] $ respectively.

$|J|=|\dfrac{d\epsilon}{dy}|=\frac{\beta}{y}$. Then under the change of variable, I have boiled (1) down to...

$$\int_{0}^{\infty}\dfrac{1}{1-e^{-x}}\left(\int_{\mu-\beta\ln x-c}^{\infty}\left[c+\mu-\beta\ln y\right]e^{-y}dy\right)e^{-x}dx$$

There might be an algebra mistake but I still cannot solve this integral...

---

RELATED QUESTION: Expectation of the Maximum of iid Gumbel Variables

Answer 1

Since the parameters $(\mu,\beta)$ of the Gumbel distribution are location and scale, respectively, the problem simplifies into computing $$\mathbb{E}[\epsilon_1|\epsilon_1+c>\epsilon_0]= \frac{\int_{-\infty}^{+\infty} x F(x+c) f(x) \text{d}x}{\int_{-\infty}^{+\infty} F(x+c) f(x) \text{d}x}$$ where $f$ and $F$ are associated with $\mu=0$, $\beta=1$. The denominator is available in closed form \begin{align*} \int_{-\infty}^{+\infty} F(x+c) f(x) \text{d}x &= \int_{-\infty}^{+\infty} \exp\{-\exp[-x-c]\}\exp\{-x\}\exp\{-\exp[-x]\}\text{d}x\\&\stackrel{a=e^c}{=}\int_{-\infty}^{+\infty} \exp\{-(1+a)\exp[-x]\}\exp\{-x\}\text{d}x\\&=\frac{1}{1+a}\left[ \exp\{-(1+a)e^{-x}\}\right]_{-\infty}^{+\infty}\\ &=\frac{1}{1+a} \end{align*} The numerator involves an exponential integral since (according to WolframAlpha integrator) \begin{align*} \int_{-\infty}^{+\infty} x F(x+c) f(x) \text{d}x &= \int_{-\infty}^{+\infty} x \exp\{-(1+a)\exp[-x]\}\exp\{-x\}\text{d}x\\ &\stackrel{z=e^{-x}}{=} \int_{0}^{+\infty} \log(z) \exp\{-(1+a)z\}\text{d}z\\ &= \frac{-1}{1+a}\left[\text{Ei}(-(1+a) z) -\log(z) e^{-(1+a) z}\right]_{0}^{\infty}\\ &= \frac{\gamma+\log(1+a)}{1+a} \end{align*} Hence $$\mathbb{E}[\epsilon_1|\epsilon_1+c>\epsilon_0]=\gamma+\log(1+e^{-c})$$ This result can easily be checked by simulation, since producing a Gumbel variate amounts to transforming a Uniform (0,1) variate, $U$, as $X=-\log\{-\log(U)\}$. Monte Carlo and theoretical means do agree:

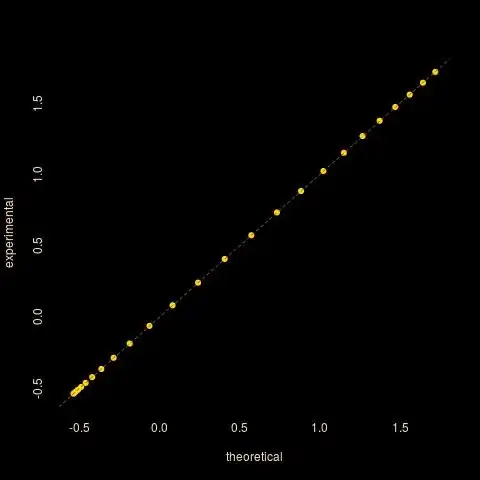$c$ varies from -2 to 2, with logarithmic axes, based on 10⁵ simulations" />

Answer 2

Xi'an computed the answer more directly by evaluating the integrals. We could also get to the answer by arguing that the conditional distribution, when scaled appropriately, is a type 1 Gumbel distribution.

---

The distribution of $\epsilon_1$ conditional on $\epsilon_1 +c > \epsilon_0$, let's call it $\epsilon_2$, is proportional to the product of a pdf and cdf

$$f_{\epsilon_2}(\epsilon_2) \propto f_{\epsilon_1}(\epsilon_2) \cdot F_{\epsilon_0}(\epsilon_2+c)$$

This will be (with $z =\frac{\epsilon_2-\mu}{\beta}$ and $d = c/\beta$)

$$f_{\epsilon_2}(\epsilon_2) \propto e^{-(z+e^{-z})} \cdot e^{-e^{-z-d}} = e^{-(z+(1+e^{-d})e^{-z})} $$

This is like a type 1 Gumbel distribution or like the more general distribution function

$$f(x) = \frac{b^a}{\Gamma(a)} e^{-(ax+be^{-x})}$$

the mean is for $a=1$ equal to $\mu_{x} = \log (b) +\gamma$ with $\gamma$ the Euler-Mascheroni constant (see below for more details). Then the mean of $z$ is

$$\mu_{z} = \log (1+e^{-c/\beta}) + \gamma$$

and the mean of $\epsilon_2$ is

$$\mu_{\epsilon_2} = \log(1+e^{-c/\beta})\beta + \gamma\beta + \mu$$

Generalized Gumbel distribution and it's mean

This form $e^{-(ax+be^{-x})}$ occurs in Ahuja, J. C., and Stanley W. Nash. "The generalized Gompertz-Verhulst family of distributions." Sankhyā: The Indian Journal of Statistics, Series A (1967): 141-156.

Although the more well known 'Gumbel distribution' is with $a=b=1$, Gumbel studied this type of distribution in 1935 (Les valeurs extrêmes des distributions statistiques) for the distribution of the m-th order observation in a sample, and he used $a=b=m$ with $m$ a positive integer.

The moment generating function is given by Ahuja and Nash:

$$M(t;a,b) = \frac{1}{\Gamma(a)}b^t\Gamma(a-t)$$

and the mean has a closed form expression when $a$ is a positive integer

$$\mu_{X,a,b} = M^\prime(0;a,b) = \log (b) + \left( \gamma - \sum_{k=1}^{a-1} \frac{1}{k} \right)$$

in the case of $a=1$ this is

$$\mu_{X,1,b} = \log (b) + \gamma $$