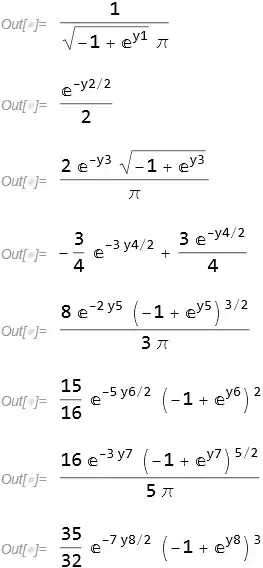Distribution with a given moment generating function

Question

As a follow-up to a question on a central limit theorem for independent random variables (r.v.) here, let $Y_j=-\log(1-V_j)$, where $V_j\sim\mbox{beta}(1-\sigma,j\sigma)$, $j\in\mathbb{N}^*$, $\sigma\in(0,1)$. The shifted sums $S_n=\sum_{j=1}^{n}Y_j -\frac{1-\sigma}{\sigma}\log n$ have moment generating functions (MGF) which admit a simple limit when $n\rightarrow \infty$: $$\mathbb{E}\left(e^{\lambda S_n}\right)\rightarrow M(\lambda)=\frac{\Gamma(1-\lambda/\sigma)}{\sigma^\lambda \Gamma(1-\lambda)}.$$

I'm trying to work out to the r.v. $S$ that admits $M(\lambda)$ as a MGF. The existence of $S$ is by the Kolmogorov three-series theorem, which ensures a.s. convergence. Note that $S$ is infinitely divisible since it is the limit of the infinitely divisible $Y_j$s.

In the expression of $M(\lambda)$, $\sigma^\lambda\Gamma(1-\lambda)$, resp. $\Gamma(1-\lambda/\sigma)$, is the MGF of a Gumbel r.v. shifted by $\log(\sigma)$, resp. Gumbel r.v. rescaled by $\sigma$. Though I don't see how to make use of this ratio since the inverse of an MGF isn't an MGF.

Answer 1

There is an explicit density for $S_n$ when $\sigma=1/2$ and a limiting density of

$$\frac{e^{-\frac{z}{2}-\frac{e^{-z}}{2}}}{\sqrt{2 \pi }}$$

(And there might be a general density for other values of $\sigma$.) I have to confess ignorance of what extreme value distribution has the above density. It's similar to a Gumbel distribution not quite.

This is done with a brute force approach where the pdf of $\sum_{i=1}^n Y_i$ is found followed by the density of $S_n=\sum_{i=1}^n Y_i - \log(n)$ (again, just for $\sigma=1/2$). Then the limit of the density of $S_n$ is found along with the limiting moment generating function.

First, the distribution of $Y_i$ (using Mathematica throughout).

pdf[j_, y_] := Simplify[PDF[TransformedDistribution[-Log[1 - x],
  x \[Distributed] BetaDistribution[1 - 1/2, j /2]], y] // 
  TrigToExp, Assumptions -> y > 0]

So the pdf for $Y_1$ and $Y_2$ are

pdf[1, y1]

$$\frac{1}{\pi \sqrt{e^{y_1}-1}}$$

pdf[2, y2]

$$\frac{e^{-\frac{y_2}{2}}}{2 \sqrt{e^{y_2}-1}}$$

The distribution of the sums of the $Y$'s are constructed sequentially:

pdfSum[1] = pdf[1, y1]
pdfSum[2] = Integrate[pdfSum[1] pdf[2, y2 - y1], {y1, 0, y2}, Assumptions -> y2 > 0]
pdfSum[3] = Integrate[pdfSum[2] pdf[3, y3 - y2], {y2, 0, y3}, Assumptions -> y3 > 0]
pdfSum[4] = Integrate[pdfSum[3] pdf[4, y4 - y3], {y3, 0, y4}, Assumptions -> y4 > 0]
pdfSum[5] = Integrate[pdfSum[4] pdf[5, y5 - y4], {y4, 0, y5}, Assumptions -> y5 > 0]
pdfSum[6] = Integrate[pdfSum[5] pdf[6, y6 - y5], {y5, 0, y6}, Assumptions -> y6 > 0]
pdfSum[7] = Integrate[pdfSum[6] pdf[7, y7 - y6], {y6, 0, y7}, Assumptions -> y7 > 0]
pdfSum[8] = Integrate[pdfSum[7] pdf[8, y8 - y7], {y7, 0, y8}, Assumptions -> y8 > 0]

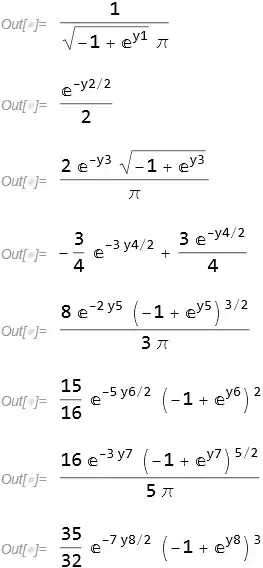
We see the pattern and the pdf for a general $n$ is

$$\frac{\Gamma \left(\frac{n+1}{2}\right) \exp \left(\frac{1}{2} (-(n-1)) z\right) (\exp (z)-1)^{\frac{n-2}{2}}}{\sqrt{\pi } \Gamma \left(\frac{n}{2}\right)}$$

So the pdf for $S_n$ is that of the above but including the shift of $\log(n)$:

pdfSn[n_] := Gamma[(1 + n)/2]/(Sqrt[\[Pi]] Gamma[n/2])*
   Exp[-(n - 1) (z + Log[n])/2] (-1 + Exp[z + Log[n]])^((n - 2)/2)

Taking the limit of this function we have

pdfS = Limit[pdfSn[n], n -> \[Infinity], Assumptions -> z \[Element] Reals]

$$\frac{e^{-\frac{z}{2}-\frac{e^{-z}}{2}}}{\sqrt{2 \pi }}$$

The moment generating function associated with this pdf is

mgf = Integrate[Exp[\[Lambda] z] pdfS, {z, -\[Infinity], \[Infinity]},
   Assumptions -> Re[\[Lambda]] < 1/2]

$$\frac{2^{-\lambda } \Gamma \left(\frac{1}{2}-\lambda \right)}{\sqrt{\pi }}$$

This doesn't look exactly like the mgf in the OP's question when $\sigma=1/2$ but Mathematica declares them identical with

Gamma[1 - \[Lambda]/(1/2)]/((1/2)^\[Lambda] Gamma[1 - \[Lambda]]) // FunctionExpand

$$\frac{2^{-\lambda } \Gamma \left(\frac{1}{2}-\lambda \right)}{\sqrt{\pi }}$$

Another check involves extracting several moments which gives identical results. Here is for the first moment:

D[mgf, {\[Lambda], 1}] /. \[Lambda] -> 0 // FunctionExpand // FullSimplify
D[Gamma[1 - \[Lambda]/(1/2)]/((1/2)^\[Lambda] Gamma[1 - \[Lambda]]), {\[Lambda], 1}] /. \[Lambda] -> 0

Both give $\gamma +\log (2)$ (where $\gamma$ is Euler's constant).

For the 17th moment:

D[mgf, {\[Lambda], 17}] /. \[Lambda] -> 0 // N
D[Gamma[1 - \[Lambda]/(1/2)]/((1/2)^\[Lambda] Gamma[1 - \[Lambda]]), {\[Lambda], 17}] /. \[Lambda] -> 0 // N

Both give 3.71979*10^19.

There might be some simple way to insert $\sigma$ into the limiting pdf but I haven't played with that yet.

Answer 2

Solution for the case $\sigma = 1/k$ with $k \in \mathbb{N}$

The answer of JimB for the case of $\sigma = 1/2$ can be adjusted in order to get to an expression for the cases $\sigma = 1/k$ where $k$ is an integer with $k \geq 2$.

In terms of $k$, the moment generating function is

$$ M(\lambda)=\frac{k^\lambda\Gamma(1-k \lambda)}{ \Gamma(1-\lambda)} = \frac{k^\lambda\Gamma(-k \lambda)\cdot(-k\lambda)}{ \Gamma(-\lambda)\cdot(-\lambda)} = \frac{k^{\lambda+1}\Gamma(-k \lambda)}{ \Gamma(-\lambda)} $$

For the derivation of the end result we will be using Gauss's multiplication formula and the generalized Gumbel distribution.

Gauss's multiplication formula

With Gauss's multiplication formula, we can write a gamma function with a parameter $k\lambda$ in terms of gamma functions with parameter $\lambda$

$$\Gamma(k\lambda) = k^{k\lambda -\frac{1}{2}} (2\pi)^{\frac{1-k}{2}} \prod_{j=0}^{k-1} \Gamma\left(\frac{j}{k} + \lambda \right)$$

And when we take the $j=0$ term in the product to the left hand side and inverse the parameter (use $-\lambda$ instead of $\lambda$)

$$\frac{\Gamma(-k\lambda)}{\Gamma(-\lambda)} = k^{-k\lambda -\frac{1}{2}} (2\pi)^{\frac{1-k}{2}} \prod_{j=1}^{k-1} \Gamma\left( \frac{j}{k} - \lambda \right)$$

If we substitute this into the moment generating function then

$$M(\lambda) = k^{\frac{1}{2}} (2\pi)^{\frac{1-k}{2}} \prod_{j=1}^{k-1} \left( \frac{1}{k}\right)^{\lambda} \Gamma\left(\frac{j}{k} - \lambda \right) $$

Generalized Gumbel distribution

The expression in the product is like the generalized Gumbel distribution

$$f(x) = \frac{b^a}{\Gamma(a)} e^{-(ax+be^{-x})}$$

with moment generating function

$$M(\lambda;a,b) = \frac{1}{\Gamma(a)}b^\lambda\Gamma(a-\lambda)$$

A description of this generalized Gumbel distribution occurs in Ahuja, J. C., and Stanley W. Nash. "The generalized Gompertz-Verhulst family of distributions." Sankhyā: The Indian Journal of Statistics, Series A (1967): 141-156.

Sum of generalized Gumbel distributions

The term $$\prod_{j=1}^{k-1} \left( \frac{1}{k}\right)^{\lambda} \Gamma\left(\frac{j}{k} - \lambda \right)$$ relates to a product of moment generating functions of the generalized Gumbel distribution with $a = j/k$ and $b=\frac{1}{k}$.

This product of moment generating functions of the gumbel distribution will involve a constant based on a product of gamma functions which we can simplify with the multiplication formula

$$\prod_{j=1}^{k-1} {\Gamma(j/k+z)} = (2\pi)^{\frac{ k-1}{2}} k^{1/2-kz} \frac{\Gamma(kz)}{\Gamma(z)} $$

setting $z=0$

$$\prod_{j=1}^{k-1} {\Gamma(j/k)} = (2\pi)^{\frac{ k-1}{2}} k^{1/2}$$

And the inverse

$$\prod_{j=1}^{k-1} \frac{1} {\Gamma(j/k)} = (2\pi)^{\frac{1-k}{2}} k^{-1/2}$$

this equals $1/k$ times the constant $k^{\frac{1}{2}} (2\pi)^{\frac{1-k}{2}} $ that we have in the moment generating function that we are looking for.

So we can write

$$ M(\lambda)=\frac{k^\lambda\Gamma(1-k \lambda)}{ \Gamma(1-\lambda)} = \frac{1}{k} \prod_{j=1}^{k-1} \frac{1} {\Gamma(j/k)} \left( \frac{1}{k}\right)^{\lambda} \Gamma\left(\frac{j}{k} - \lambda \right) $$

The product on the right-hand side is the product of the moment generating function of generalized Gumbel distributions with $a = j/k$ and $b=\frac{1}{k}$. The factor $1/k$ relates to a translation with a factor $-\log(k)$.