7

This seems like a common problem but I cannot find a solution.

I have a set of binary observations and two different models, each with predictions for each observation. I want to compare the calibration of the models.

There are several approaches to comparing the discrimination of these models (i.e. see the roc.test in the pROC package in R), but no approach to compare calibration. Most empirical papers just list the p-values from two different calibration tests that are testing whether each model's calibration is off (i.e. Hosmer-Lemeshow, Brier score).

What I am looking for is a direct statistical comparison of the calibration between two models.

Here's an extreme test data set. The values of the Brier test, Spiegelhalter Z-test, etc all support that p2 is better calibrated, and we know it is. Can anyone make this into a formal statistical test? 

library("pROC")
y <- rbinom(100,1,1:100/100)
p1 <- 1:100/10001
p2 <- 1:100/101
val.prob(p1,y)
val.prob(p2,y)
kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
R_G
  • 81
  • 5
  • I am not sure I know what you mean by calibration. Can you expand on what you mean by that? Maybe it is known under a different name in another literature – Jeremias K Dec 16 '17 at 17:10

2 Answers2

4

As you know the Brier score measures calibration and is the mean square error, $\bar B = n^{-1} \sum (\hat y_i - y_i)^2$, between the predictions, $\hat y,$ and the responses, $y$. Since the Brier score is a mean, comparing two Brier scores is basically a comparison of means and you can go as fancy with it as you like. I'll suggest two things and point to a third:

One option: do a t-test

My immediate response when I hear comparisons of means is to do a t-test. Squared errors probably aren't normally distributed in general so it's possible that this isn't the most powerful test. It seems fine in your extreme example. Below I test the alternative hypothesis that p1 has greater MSE than p2: 

y <- rbinom(100,1,1:100/100)
p1 <- 1:100/10001
p2 <- 1:100/101

squares_1 <- (p1 - y)^2
squares_2 <- (p2 - y)^2

t.test(squares_1, squares_2, paired=T, alternative="greater")
#> 
#>  Paired t-test
#> 
#> data:  squares_1 and squares_2
#> t = 4.8826, df = 99, p-value = 2.01e-06
#> alternative hypothesis: true difference in means is greater than 0
#> 95 percent confidence interval:
#>  0.1769769       Inf
#> sample estimates:
#> mean of the differences 
#>               0.2681719

We get a super-low p-value. I did a paired t-test as, observation for observation, the two sets of predictions compare against the same outcome.

Another option: permutation testing

If the distribution of the squared errors worries you, perhaps you don't want to make assumptions of a t-test. You could for instance test the same hypothesis with a permutation test:

library(plyr)

observed <- mean(squares_1) - mean(squares_2)
permutations <- raply(500000, {
  swap <- sample(c(T, F), 100, replace=T)
  one <- squares_1
  one[swap] <- squares_2[swap]

  two <- squares_2
  two[swap] <- squares_1[swap]

  mean(one) - mean(two)
})

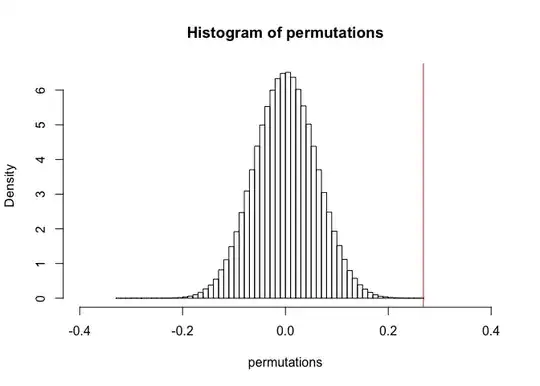
hist(permutations, prob=T, nclass=60, xlim=c(-.4, .4))
abline(v=observed, col="red")


# p-value. I add 1 so that the p-value doesn't come out 0
(sum(permutations > observed) + 1)/(length(permutations) + 1) 
#> [1] 1.999996e-06

The two tests seem to agree closely.

Some other answers

A quick search of this site on comparison of MSEs point to the Diebold-Mariano test (see the answer here, and a comment here). This looks like it's simply Wald's test and I guess it will perform similarly to the t-test above.

einar
  • 3,258
  • 2
  • 19
  • 31
  • 1
    Just some food for thought (which I'm also not so sure about myself): to me this does not seem as a comparison of Brier scores, but as a comparison of model residuals. IMO this is pretty smart and straightforward, but do remember that where there is one model which predicts pretty accurate at lower predicted probabilities, and another model which predicts accurately at high predicted probabilities, they might seem to have equal performance. So, without taking into account some prior knowledge on the most important region, I'd recommend to look at the calibration plots as well. – IWS Dec 18 '17 at 15:37
  • @IWS thank you for your comment. I guess it might depend on where the question's predictions come from? Presumably I would be comparing average residuals if they come from the same data to which the model was fit and proper Brier scores if they come from, eg, cross-validation or some new data set. Unless I misunderstand you. I agree about your point about the most important region: it's possible to have decent calibration with an intercept-only model but predictions would be useless. – einar Dec 19 '17 at 12:16
  • Thank-you for your excellent answer einar. Very helpful. – R_G Dec 27 '17 at 15:44
0

For future reference, IMO the first answer does not address the calibration issue. Consider predictions $ \hat{y}_1,\hat{y}_2 ..., \hat{y}_n $ made by a reasonable, well calibrated, model for input values $x_1, x_2,..., x_n$. Now consider a second set of predictions $\tilde{y}_1, \tilde{y}_2, ..., \tilde{y}_n$ that are made by a model that simply scrambles the predictions of the first model within each of the two classes and outputs them in random order. The second model is likely to be poorly calibrated compared to the first well calibrated model, but the brier scores of the two models will be the same.

As stated in the original question, I suggest looking at the Hosmer–Lemeshow test, and comparing the HL test-statistics computed for the predictions of each of the two models (A larger HL statistic suggests poorer calibration).

YBE
  • 1