I did some tutorials and read few articles but still have a problem with SVM, exactly with SVR. I'm doing analysis in R and I use e1071 library with "svm" function. Into that function I use my multivariable equation, so svm works since now like SVR.
My results:
(general: cost=1,gamma=0.1666)
-epsilon=0.1(61 SV-supported vectors) - RMSE = 4.1(on unseen data)
-epsilon=1(10 SV) - RMSE = 19(on unseen data)
-epsilon=1.3(7 SV) - RMSE = 25(on unseen data)
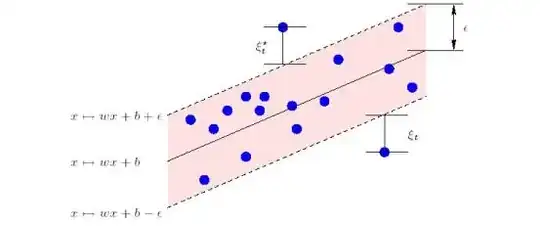
When epsilon is increasing I understand that we should have actually more supported vectors as we can see on the picture below:
In our case as we can see the bigger epsilon the less supported vectors. I don't know why this happens. I would be glad if someone can explain it to me.